Читайте также:
|
Рассматривать обычное евклидово расстояние на плоскости:
(
) 
.
В этом случае зоны Дирихле нетрудно построить для любого числа точек. Так как серединный перпендикуляр является геометрическим местом точек равноудалённых от двух данных, то двух точек достаточно соединить их отрезком и провести серединный перпендикуляр. Эта прямая и будет делить пространство на зоны Дирихле (рис. 3.6).
 |
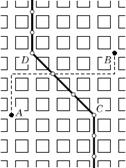Рис 3.6 Рис 3.7
Зоны Дирихле возникают во многих прикладных задачах. Например, пусть необходимо разделить город на зоны Дирихле относительно станций метро. Воспользуемся метрикой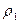 
(
). Представим сетку улиц с правильной планировкой и две станции метро А и В (рис 3.7).
Здесь разделителем плоскости на сферы влияния будет множество точек, от которых до станции А и В будет одинаковое расстояние. В это множество попадают точки отрезка CD, которые являются серединами кратчайшего пути от станции метро А до станции метро В (один из них показан пунктиром на рис. 3.7). Далее при перемещении вдоль линии-разделителя ниже точки С или выше D путь увеличивается на 1 квартал.
Зоны Дирихле также используются в теории кодирования. Пусть, например, нужно автоматически исправлять ошибки при передаче закодированных сообщений. Рассмотрим слова, записанные в двоичной системе счисления (0,1) и состоящие из 5 букв. За расстояние примем количество побуквенных различий в словах. Например, расстояние от 01011 и 11101 равно 3. В реальности используются более длинные слова. В качестве центров притяжения используются только осмысленные слова.
Так, если произошел сбой в передаче, то некоторые слова изменились на близкие к ним. А так как всё пространство делено на Зоны Дирихле относительно осмысленных слов, то мы можем изменить сообщение, заменяя слова с ошибками на ближайшие к ним. Именно так работают некоторые механизмы автоматического исправления в теории кодирования [1].
Дата добавления: 2015-07-25; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аксиомы метрики | | | Интересный факт |