Интересный факт

Лемма. Дан и произвольная точка Х внутри него. Точку Х отразили симметрично относительно середин сторон треугольника. Отрезки соединяют вершины исходного треугольника с отражениями точки Х (рис. 2.5). Оказывается, что построенные таким образом прямые пересекутся в одной точке.

Отметим, что похожее утверждение имеется в [8] и доказывается с помощью подобия треугольников.

Доказательство

Точка 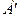не может лежать на продолжении ВС потому, что тогда или , что невозможно.

Точка не может лежать на продолжении АС потому, что тогда или , что невозможно.

Точка не может лежать на продолжении АВ потому, что тогда или , что невозможно.

1) По теореме Чевы:

Если , то отрезки пересекаются в одной точке.

2) 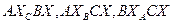— параллелограммы, так как точкой пересечения диагонали делятся на равные части. Из этого следует, что:

А) , ,

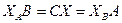Б) , , , следовательно

,

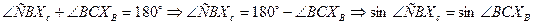
3) , ,

, ,

, .

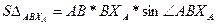4) , , , значит

.

Значит, и прямые пересекаются в одной точке, что и требовалось доказать. Так же необходимо отметить, что если Х – центроид , то точка пересечения этих прямых совпадает с точкой Х.

Дата добавления: 2015-07-25