Время жизни возбужденного состояния молекул. Связь между временем жизни возбужденных состояний и квантовым выходом фотолюминесценции.

k

Поскольку молекулы в состоянии электронного возбуждения обладают избытком свободной энергии, они термодинамически не стабильны. Поэтому после прекращения генерации новых возбужденных молекул в объекте (например, после выключения источника возбуждающего света) их концентрация начинает быстро снижаться. Если мы обозначим возбужденные молекулы в объекте, как Р^*, то процесс исчезновения таких молекул можно представить в виде химической реакции:

(66)

Р^* Р

В этом уравнении k – суммарная константа скорости всех процессов, в которых расходуются (инактивируются) возбужденные молекулы.

Согласно правилам химической кинетики, изменение концентрации возбужденных молекул в образце (d[P^*]) за время dt будет равно:

(67)

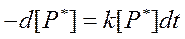
Решим полученное дифференциальное уравнение (67):

(68)

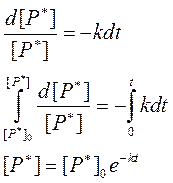
В представленных выражениях [P^*]₀ – концентрация возбужденных молекул в момент прекращения их генерации (момент времени t =0). Из уравнения (68) следует, что после прекращения генерации новых возбужденных молекул их концентрация в объекте будет экспоненциально снижаться со временем.

Константа скорости инактивации возбужденных молекул k имеет размерность 1/с. Введем величину t = 1/k. Обозначим ее как реальное время жизни возбужденных состояний в образце и выразим с ее помощью зависимость [P^*] от времени, преобразовав выражение (68):

(69)

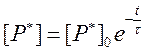
Определим, насколько измениться [P^*] к моменту времени t=t:

(70)

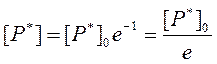
Из уравнения (70) следует, таким образом, что к моменту времени t=t концентрация возбужденных молекул в образце после прекращения их генерации de novo снизится относительно исходной концентрации в е раз (е – основание натуральных логарифмов, равное 2,7182818284 5904523536…).

Константа скорости инактивации возбужденных молекул k вводилась нами, как суммарная константа скоростей всех процессов, в ходе которых эти молекулы расходуются. Иными словами, k=k₁+k₂+k₃+…+k_n, где k₁, k₂, k₃ и т.д. - константы скорости каждого из процессов, сопровождающихся исчезновением молекул в состоянии возбуждения в объекте. Пусть при этом k₁ – константа скорости излучательного тушения таких молекул:

	k1

(71)

Р^* Р+hn

Тогда можно выразить интенсивности фотолюминесценции образца через концентрации возбужденных молекул в нем следующим образом:

(72)

(73)

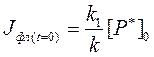
Подставив выражение [P^*] и [P^*]₀ через соответствующие значения J_фл из уравнений (72) и (73), в уравнение (69), получим

(74)

Иными словами, интенсивность фотолюминесценции объекта после прекращения его возбуждения также, как и концентрация возбужденных молекул в образце, будет снижаться со временем экспоненциально. Это дает возможность определения величины t (реального времени жизни возбужденных состояний в образце) экспериментально. Для определения t нужно зарегистрировать кинетику затухания фотолюминесценции после выключения источника возбуждающего света, и определить время, за которое J_фл снижается в е раз. Следует заметить, что это сделать бывает непросто – напомним, что синглетно-возбужденные молекулы при обычных условиях существуют не более 10^-12-10^-8 с. Поэтому для регистрации кинетик затухания фотолюминесценции требуются чрезвычайно быстродействующие приборы, с константой времени реагирования порядка 10^-13 с. Впрочем, в последнее время для этого применяются специальные устройства – однофотонные t -метры (читается – тау-метры). В этих приборах регистрируется распределение по величине времени жизни отдельных молекул в объекте после возбуждения фотолюминесценции коротким (продолжительностью от 0,1 до 10 нс) импульсом излучения. Затем по этому распределению рассчитывается искомая величина t.

Выше уже неоднократно указывалось, что испускание кванта фотолюминесценции в обычных условиях – не единственный способ избавления от энергии электронного возбуждения для возбужденных молекул. Однако можно представить себе условия, в которых фотолюминесценция будет таковым. Действительно, если возбужденная молекула находится при температуре около абсолютного нуля и в вакууме, т.е. всякие ее взаимодействия с окружением исключены, то величина k₁ для нее будет стремиться к k. Квантовый же выход фотолюминесценции в таких условиях станет равен 1. Если рассматривать время жизни возбужденных молекул в таких, модельных, условиях, когда квантовый выход фотолюминесценции равен 1 (т.е. все возбужденные молекулы инактивируются исключительно излучательно), то этот показатель принято называть истинным временем жизни возбужденного состояния. Обозначим его t_и. Введя понятие t_и, легко составить пропорцию, показывающую взаимосвязь между реальным и истинным временами жизни возбужденных состояний, с одной стороны, и квантовым выходом фотолюминесценции – с другой.

Действительно, если величине t_и соответствует квантовый выход фотолюминесценции 1, а величине t - квантовый выход фотолюминесценции q, то:

	(75)

t=t_и q

а

(76)

q= t/t_и

Выражения (75) и (76) определяют, таким образом, как связаны квантовый выход фотолюминесценции и времена жизни возбужденных состояний молекул в объекте друг с другом.

Если мы вспомним, что понятие времени жизни возбужденного состояния вводилось нами, как величина, обратная константе скорости инактивации электронных возбуждений (т.е. t=1/k, а t_и=1/k₁, см. выше), можно также написать, что:

(77)

q=k₁/k

Следует заметить, что измерение величин t обычно осуществляется для определения типа электронного возбуждения исследуемых молекул в объекте. Это бывает необходимо, например, при выяснении того, какая именно молекула в объекте может опосредовать фотохимические реакции, определяющие тот или иной фотобиологический эффект.

Как уже указывалось выше, при триплетном возбуждении обратный переход Т ® S₀ требует от электрона изменения спина, т.е. дополнительных затрат энергии. Поэтому триплетно-возбужденные молекулы живут в состоянии возбуждения намного дольше, чем синглетно-возбужденные (напомним, что для синглетных возбуждений время жизни составляет 10^-8 ¸10^-12 секунды, а для триплетных – от 10^-7 секунды до целых секунд). Это высказывание относится, впрочем, только к величинам t_и рассматриваемых типов возбужденных молекул. Дело здесь в том, что и у синглетных, и у триплетных возбужденных состояний время жизни существенно зависит от наличия возможности безизлучательного избавления от избытка свободной энергии. С ростом температуры такая возможность появляется (k₁ перестает быть равным k, поскольку появляются процессы инактивации возбуждений с константами скоростей k₂, k₃ и т.д.). Поэтому t всегда оказывается меньше, чем t_и. Однако, из-за того, что t_и у триплетно-возбужденных молекул изначально больше, эти молекулы успевают за время жизни в возбужденном состоянии сместиться от места образования дальше (чем синглетно-возбужденные), и для них вероятность безизлучательного тушения (например, путем растраты энергии в ходе соударений с другими молекулами) с ростом температуры увеличивается значительно быстрее. Из-за этого, в частности, зарегистрировать фосфоресценцию большинства биологических объектов при комнатной температуре (порядка 300^о К) из-за ее малой интенсивности очень сложно. Большая величина t_и, кроме того, позволяет молекулам в состоянии триплетного возбуждения, в сравнении с синглетно-возбужденными, чаще вступать в фотохимические реакции. Поэтому многие фотобиологические процессы оказываются связаны с фотохимическим превращениями, опосредуемыми именно триплетно-возбужденными молекулами.

Важно заметить, что величина константы скорости излучательного перехода в возбужденных молекулах (k₁) зависит от способности молекул данного типа поглощать излучение в основном состоянии:

(78)

В выражении (78) v – волновое число излучения (v=1/l), v_м – величина волнового числа в максимуме поглощения, интеграл – площадь под кривой спектра поглощения (для одной полосы поглощения этот интеграл составляет» e_мDv_1/2, e_м – величина молярного коэффициента поглощения в максимуме рассматриваемой полосы, Dv_1/2 – ее полуширина). Из уравнения (78) вытекает, что величина t_и падает, если возбуждение молекул осуществляется излучением в интенсивных максимумах их спектров поглощения.

---

Дата добавления: 2015-07-25