Читайте также:
|
Если в ходе исследования знакочередующейся последовательности 
получен бесконечный результат 
(или если предела нет), то у последовательности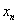 
предела не существует вообще. Такой инцидент напоминает историю с 
.
Наше увлекательное путешествие в мир последовательностей подошло к концу и, надеюсь, оно составило достойную конкуренцию Вконтакте =) =) =)
Успехов в учёбе!
Решения и ответы:
Пример 2: Решение:
Найдём предел последовательности:
Используем формулу суммы 
первых членов арифметической прогрессии 
.
В данном случае 
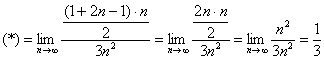
Пример 4: Решение:
Пример 6: Решение:
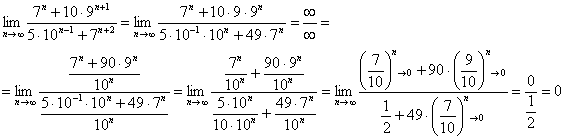
Пример 8: Решение:
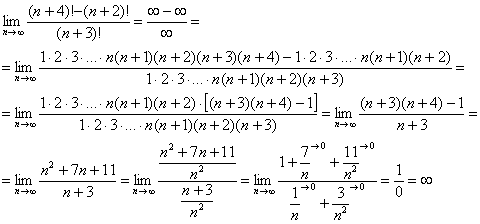
Пример 10: Решение: последовательность 
– ограничена: 
, а последовательность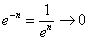 
, значит, по соответствующей теореме:
Пример 12: Решение:
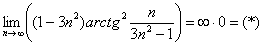
Заменим бесконечно малую эквивалентно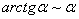й: 
при 
.
В данном примере 
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Дата добавления: 2015-07-25; просмотров: 38 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Как найти предел знакочередующейся последовательности? | | | Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений. |