Теорема: произведение ограниченной последовательности на бесконечно малую последовательность – есть бесконечно малая последовательность.

Если вам не очень понятен термин «ограниченность», пожалуйста, изучите статью об элементарных функциях и графиках.

Аналогичная теорема справедлива, кстати, и для функций: произведение ограниченной функции на бесконечно малую функцию – есть бесконечно малая функция.

Пример 9

Найти предел последовательности

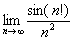
Решение: последовательность – ограничена: , а последовательность – бесконечно малА, значит, по соответствующей теореме:

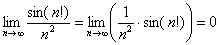
Просто и со вкусом. Да-да, так и оформляем.

А почему бы и нет?

Пример 10

Найти предел последовательности

Это пример для самостоятельного решения.

Ещё две распространённые ограниченные функции – арктангенс и арккотангенс:

Аргументы перечисленных тригонометрических функций могут быть заполнены знатной абракадаброй, но это не должно приводить в панику – существенно то, что последовательности ограничены!

Иногда в ходе вычисления пределов последовательностей приходится использовать довольно неожиданные приёмы:

Пример 11

Найти предел последовательности

Решение: неопределённость можно раскрутить двумя способами. Первый путь – через первый замечательный предел, который справедлив, как ни странно, и для последовательностей:

(1) Используем формулу .

(2) Избавляемся от косинуса, указывая, что он стремится к единице.

(3) Неопределённость не устранена, но теперь вместо тангенса у нас синус, и появляется возможность организовать 1-ый замечательный предел. Проводим стандартный искусственный приём: делим всё выражение на 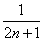и, чтобы ничего не изменилось, домножаем на .

(4) Используем первый замечательный предел , при этом, в качестве бесконечно малой величины выступает , которая, понятно, стремится к нулю при .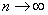

Дальнейшее просто.

Прокатывает и 2-ой метод решения – через замечательные эквивалентности:

Заменим бесконечно малую последовательность эквивалентной:
при .
В данном случае

Готово.

Пример 12

Найти предел последовательности

Это пример для самостоятельного решения. Здесь аргумент арктангенса также бесконечно мал, поскольку его знаменатель более высокого порядка роста, чем числитель. Решать, разумеется, значительно выгоднее через замечательную эквивалентность.

Оба рассмотренных примера справедливы и для функций, похожие пределы также разобраны в Примерах 12-13 урока о бесконечно малых величинах.

В заключение урока рассмотрим ещё один важный вопрос:

Дата добавления: 2015-07-25