Как найти предел последовательности?

А вот сейчас необходимо уметь решать пределы функций, как минимум, на уровне двух базовых уроков: Пределы. Примеры решений и Замечательные пределы. Потому что многие методы решения будут похожи. Но, прежде всего, проанализируем принципиальные отличия предела последовательности от предела функции:

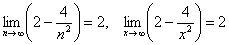
В пределе последовательности «динамическая» переменная «эн» может стремиться только к «плюс бесконечности» – в сторону увеличения натуральных номеров 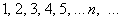. В пределе функции «икс» можно направить куда угодно – к «минус бесконечности» либо к произвольному действительному числу.

Последовательность дискретна (прерывна), то есть состоит из отдельных изолированных членов. Раз, два, три, четыре, пять, вышел зайчик погулять. Для аргумента же функции характерна непрерывность, то есть «икс» плавно, без приключений стремится к тому или иному значению. И, соответственно, значения функции будут так же непрерывно приближаться к своему пределу.

По причине дискретности в пределах последовательностей встречаются свои фирменные вещи, которые теряют всякий смысл для традиционных функций. Например, факториалы, «мигалки», прогрессии. Иными словами, не бывает «икс факториала» или «икса в степени минус один». И сейчас я постараюсь разобрать пределы, которые свойственны именно для последовательностей.

Начнём с прогрессий:

Пример 1

Найти предел последовательности

Решение: нечто похожее на бесконечно убывающую геометрическую прогрессию, но она ли это? Для ясности распишем несколько первых членов:

Так как 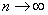, то речь идёт о сумме членов бесконечно убывающей геометрической прогрессии, которая рассчитывается по формуле .

Оформляем решение:

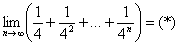
Используем формулу суммы бесконечно убывающей геометрической прогрессии: . В данном случае: – первый член, – знаменатель прогрессии.

Главное, совладать с четырёхэтажностью дроби:

Есть.

Пример 2

Написать первые четыре члена последовательности и найти её предел

Это пример для самостоятельного решения. Для устранения неопределённости 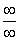в числителе потребуется применить формулу суммы первых членов арифметической прогрессии:
, где 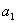– первый, а – энный член прогрессии.

Поскольку в пределах последовательностей «эн» всегда стремится к «плюс бесконечности», то неудивительно, что неопределённость 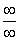– одна из самых популярных.
И многие примеры решаются точно так же, как пределы функций!

Как вычислить эти пределы? Смотрите Примеры №№1-3 урока Пределы. Примеры решений.

А может быть что-нибудь посложнее наподобие 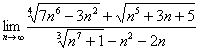? Ознакомьтесь с Примером №3 статьи Методы решения пределов.

С формальной точки зрения разница будет лишь в одной букве – там «икс», а здесь «эн».
Приём тот же – числитель и знаменатель надо разделить на «эн» в старшей степени.

Также в пределах последовательностей достаточно распространена неопределённость . Как решать пределы вроде можно узнать из Примеров №11-13 той же статьи.

Чтобы разобраться с пределом , обратитесь к Примеру №7 урока Замечательные пределы (второй замечательный предел справедлив и для дискретного случая). Решение снова будет как под копирку с различием в единственной букве.

Следующие четыре примера (№№3-6) тоже «двулики», но на практике почему-то больше характерны для пределов последовательностей, чем для пределов функций:

Пример 3

Найти предел последовательности

Решение: сначала полное решение, потом пошаговые комментарии:

(1) В числителе дважды используем формулу .

(2) Приводим подобные слагаемые в числителе.

(3) Для устранения неопределённости делим числитель и знаменатель на («эн» в старшей степени).

Как видите, ничего сложного.

Пример 4

Найти предел последовательности

Это пример для самостоятельного решения, формулы сокращенного умножения в помощь.

В пределах с показательными последовательностями применяется похожий метод деления числителя и знаменателя:

Пример 5

Найти предел последовательности

Решение оформим по той же схеме:

(1) Используя свойства степеней, вынесем из показателей всё лишнее, оставив там только «эн».

(2) Смотрим, какие показательные последовательности есть в пределе: и выбираем последовательность с наибольшим основанием: . В целях устранения неопределённости делим числитель и знаменатель на .

(3) В числителе и знаменателе проводим почленное деление. Поскольку является бесконечно убывающей геометрической прогрессией , то она стремится к нулю. И тем более к нулю стремится константа, делённая на растущую прогрессию: . Делаем соответствующие пометки и записываем ответ.

Пример 6

Найти предел последовательности

Это пример для самостоятельного решения.

Как-то незаслуженно остался в забвении стильный почерк, присущий только пределу последовательности. Пора исправить ситуацию:

Пример 7

Найти предел последовательности

Решение: чтобы избавиться от «вечного соперника» нужно расписать факториалы в виде произведений. Но прежде, чем приступить к математическому граффити, рассмотрим конкретный пример, например:.

Последним множителем в произведении идёт шестёрка. Что нужно сделать, чтобы получить предыдущий множитель? Вычесть единицу: 6 – 1 = 5. Чтобы получить множитель, который располагается ещё дальше, нужно из пятёрки ещё раз вычесть единичку: 5 – 1 = 4. И так далее.

Не беспокойтесь, это не урок в первом классе коррекционной школы, на самом деле мы знакомимся с важным и универсальным алгоритмом под названием «как разложить любой факториал». Давайте разделаемся с самым злостным флудером нашего чата:

Очевидно, что последним множителем в произведении будет .

Как получить предыдущий множитель? Вычесть единицу:

Как достать прадедушку? Ещё раз вычесть единицу: .

Ну и ещё на один шаг продвинемся вглубь: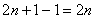

Таким образом, наше чудовище распишется следующим образом:

С факториалами числителя всё проще, так, мелкие хулиганы.

Оформляем решение:

(1) Расписываем факториалы

(2) В числителе ДВА слагаемых. Выносим за скобки всё, что можно вынести, в данном случае это произведение . Квадратные скобки, как я где-то пару раз говорил, отличаются от круглых скобок только своей квадратностью.

(3) Сокращаем числитель и знаменатель на …. …хммм, флуда тут и впрямь много.

(4) Упрощаем числитель

(5) Сокращаем числитель и знаменатель на 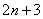. Тут в известной степени повезло. В общем случае вверху и внизу получаются заурядные многочлены, после чего приходится выполнять стандартное действие – делить числитель и знаменатель на «эн» в старшей степени.

Более подготовленные студенты, которые легко раскладывают факториалы в уме, могут решить пример значительно быстрее. На первом шаге делим почленно числитель на знаменатель и мысленно выполняем сокращения:

Но способ с разложением всё-таки более основателен и надёжен.

Пример 8

Найти предел последовательности

Это более пример для самостоятельного решения.

Желающие набить руку на рассмотренных типах пределов могут обратиться к сборнику Кузнецова. Около 150-ти прорешанных примеров можно найти здесь >>> (задачи №№2-6).

Как и в любом обществе, среди числовых последовательностей попадаются экстравагантные личности.

Дата добавления: 2015-07-25