
Читайте также:
|
Пределы
Арифметические свойства
Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
· Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.

· Однородность. Константу можно выносить из-под знака предела.

· Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.

· Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
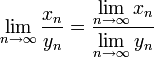
Дата добавления: 2015-07-25; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ответ: так как последовательность является знакочередующейся и , то . | | | Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа. |