
Читайте также:
|
Множество всех значений, которые может принять зависимая переменная, называется областью значения функции и обозначается E (f) или E (y).
Рассмотрим Е (у) для 1.,2.,3.,4.
1. Е (у)= (∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.
2. Е (у)= [0; +∞)// мн-во неотрицат.чисел
3. Е (у)=(∞; +∞)//всё мн-во действит.чисел
4. Е (у)= [0; +∞)// мн-во неотрицат.чисел
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областяхматематического анализа
, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f (x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.· Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
· Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
· Ни чётная ни нечётная функция (функция общего вида) — функция, не обладающая симметрией. В эту категорию относят функции, не подпадающие под предыдущие 2 категории.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
Говоря более формально, функция называется периодической, если существует такое число T≠0 (период), что на всей области определения функции выполняется равенство  .
.
Исходя из определения, для периодической функции справедливо также равенство  , где
, где 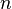 - любое целое число.
- любое целое число.
Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное[1]. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции
Пусть дана функция  Тогда
Тогда
· функция  называется возраста́ющей на
называется возраста́ющей на  , если
, если
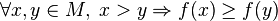 .
.
· функция  называется стро́го возраста́ющей на
называется стро́го возраста́ющей на  , если
, если
 .
.
· функция  называется убыва́ющей на
называется убыва́ющей на  , если
, если
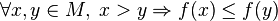 .
.
· функция  называется стро́го убыва́ющей на
называется стро́го убыва́ющей на  , если
, если
 .
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
1. Понятие о сложной функции
Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точкеу).
Пример. Функцию 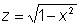 можно рассматривать как композицию функций
можно рассматривать как композицию функций  и
и  .
.
Для записи композиции функций употребляется значок 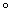 . Например, запись
. Например, запись  означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е.
означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е.  .
.
Операция образования сложной функции (или композиция функций) не обладает переместительным свойством:  .
.
Чтобы можно было вычислить сложную функцию h = f(g(x)), надо, чтобы число g(x), т. е. значение функции g, попадало в область определения функции f.
Пример. 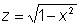
Вычисляя значения функции  , необходимо брать только те числа х, для которых
, необходимо брать только те числа х, для которых 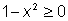 , т. е. те, для которых число
, т. е. те, для которых число  попадает в область определения функции
попадает в область определения функции  .
.
2. Взаимно обратные функции
Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у.Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f.
Если функция g является обратной для функции f, то и функция является обратной для функции g.
Пару функций f и g называют взаимно обратными функциями.
3. График обратной функции
Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат – их значения, то эти графики будут симметричны друг другу относительно прямой у = х.
4. Свойства взаимно обратных функций
Отметим некоторые свойства взаимно обратных функций.
1) Тождества. Пусть f и g – взаимно обратные функции. Тогда: f(g(y)) = у и g(f(x)) = х.
2) Область определения. Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и наоборот, область значений функции f совпадает с областью определения функции g.
3) Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное утверждение верно и для убывающих функций.
4) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой у = х.
Дата добавления: 2015-07-25; просмотров: 79 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства бесконечно малых | | | Пределы. Непрерывность функций. |