Читайте также:
|
В современных системах устройством управления, которое принимает на своих входах заданные и измеренные значения выходных параметров, значения измеряемых возмущений, содержит зависимости между входами и выходами управляемого объекта, вычисляет и подает на его вход необходимые изменения управляющих воздействий для наиболее точного выполнения задания, являются вычислительные машины. К управляющим устройствам естественно предъявить не только требование свести к нулевому уровню рассогласование между заданными и текущими значениями выходных параметров объекта, но и сделать это как можно быстрее – такие системы называют оптимальными по быстродействию.
Задача создания оптимального по быстродействию алгоритма управления очень сложна даже в простейших случаях. Как правило, управляемые процессы описываются системой нелинейных дифференциальных уравнений достаточно высокого порядка. Но пусть для простого примера замкнутая система управления в целом (объект и управляющее устройство или регулятор) описываются линейным дифференциальным уравнением второго порядка с постоянными коэффициентами. При малых значениях коэффициента демпфирования (при первой производной в дифференциальном уравнении) переходный процесс будет иметь резко колебательный характер (с большим перерегулированием) и время компенсации (например, ступенчатого возмущения по нагрузке) будет большим. Если сделать коэффициент демпфирования слишком большим, то движение к заданному значению будет апериодическим и время регулирования будет также большим. Выбором коэффициента демпфирования можно уменьшить время регулирования до некоторого значения, но простейшие соображения подсказывают, что можно достичь лучшего результата, если перейти в нелинейный режим – при больших рассогласованиях сделаем коэффициент малым, а при достаточном уменьшении рассогласования резко его увеличим: начальная фаза процесса обеспечит движение к нулевому рассогласованию с максимальной скоростью, а завершающая будет соответствовать плавному апериодическому подходу к заданию. В результате время регулирования значительно сократится.
Переходный процесс: 1 – при малом демпфировании, 2 – при сильном демпфировании, 3 – при переключении значения коэффициента демпфирования.
Системы, способные изменять свои параметры для достижения лучшего качества переходных процессов носят название систем с переменной структурой. Исследование нелинейных систем очень трудоемко, но ожидаемые результаты того стоят.
В большинстве реальных случаев объект управления задан и его характеристики изменять нельзя – в этом случае задача разработки системы управления сводится к созданию такого реализуемого управляющего алгоритма, который обеспечивает наилучшее в определенном смысле управление объектом. Структура управляющего алгоритма зависит от характеристик объекта и предъявляемых к процессу требований, объема доступной информации о процессе, ограничений на ресурсы управления (на управляющие воздействия) и на все переменные состояния объекта – координаты, скорости, ускорения и пр. Математическая модель управляемого объекта в общем случае может быть представлена системой дифференциальных уравнений вида:
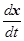= f (x, u, z, t).
Здесь х, u, z – вектор-функции от времени t выходных параметров, управляющих воздействий, измеряемых возмущений соответственно, f – вектор-функция, связывающая их взаимной зависимостью. В зависимости от того, какая группа из этих функций должна быть найдена в результате решения системы уравнений, различают следующие задачи:
ü задачу анализа (система решается относительно х);
ü задачу идентификации объекта управления (определяется f);
ü задачу определения алгоритма управления (система решается относительно u при заданных требования к нему и наложенной системе ограничений).
В этом разделе мы обсудим постановку и некоторые методы решения последней задачи.
Предъявляемые к управляемому объекту требования содержат цель управления – на языке математики это всегда желание достичь экстремума некоторой величины Q – критерия оптимальности, значение которого в общем случае зависит как от выходной величины, так и от управляющего воздействия и может явно зависеть от времени:
Q (x, u, t) =min.
Q – это функционал, число, зависящее от вида функций x, u. Например, в частном случае Q= 
, где Т – фиксированная величина.
В качестве критерия Q могут быть выбраны различные технические или экономические показатели – производительность, качество, затраты сырья или энергоресурсов: выбор за прикладной областью, а не за теорией управления.
В настоящее время продолжается построение единой общей теории оптимальных систем управления, включающей как формулировку общих задач, так и методы их решения. Рассмотрим общие задачи этой теории.
Пусть заданы: оператор объекта f (x, u, z, t), цель управления Q, ограничения на управления u ÎW(u) и/или на координаты объекта x ÎW(x). Зададимся также классом кусочно-непрерывных функций u (t) с конечным числом точек разрыва первого рода на конечном интервале. Задача состоит в том, чтобы при этих заданных условиях найти такой алгоритм (стратегию) управляющего устройства, при котором критерий оптимальности принимает минимальное значение. Такой алгоритм называют оптимальным. В частном случае систем с полной информацией об объекте, когда функции z и x регулярны и могут быть включены в состав оператора объекта и критерия оптимальности, общее выражение для алгоритма оптимальной системы имеет вид:
u (t) = K [ x (t), u (t), t ] (t 0£ t £ t).
Если текущее значение вектора x полностью характеризует все будущее поведение объекта независимо от предыстории при t £ t, объект характеризуется заданными дифференциальными уравнениями и не содержит запаздываний, то u (t) в данный момент является функцией только значения х в тот же момент времени u (t) = K [ x (t), t ]. Если, наконец, объект стационарен (уравнения движения не содержат явно время t), то оптимальный алгоритм ищется в виде функции u (t) = K [ x (t)].
Изложенная постановка задачи оптимального управления является основной. Но существует и другая задача – об определении оптимальных процессов u (t), x (t) при заданных начальных условиях х 0; это не главная задача, она выдвигается обычно в виде промежуточной, чтобы от нее перейти к основной – определению оптимального алгоритма. Исключая, например, из зависимости u (t), x (t), при некоторых дополнительных условиях можно найти зависимость u (x), то есть алгоритм оптимального управляющего устройства.
Постановку задачи определения оптимального процесса, например, для систем с полной информацией об объекте можно сформулировать так. Пусть задано векторное уравнение движения объекта
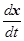= f (x, u, t),
где f i – непрерывные и дифференцируемые по своим аргументам функции, x (t 0) = x 0.
Допустимыми будем считать управления, удовлетворяющие имеющимся ограничениям u ÎW(u). В задаче об оптимальном процессе требуется найти такое допустимое u (t) и соответствующее ему движение x (t) объекта, чтобы траектория изображающей точки в фазовом пространстве системы, переходящей из начального состояния x 0 в состояние x Т обеспечивала минимум некоторому функционалу Q= 
, где G – конечная, обычно положительная скалярная функция x (t), u (t) и t. Явную зависимость от времени формально можно устранить вводом дополнительной координаты x n+ 1, x n+ 1(t= 0) = 0, 
= 1. Так как при этом x n+ 1 =t, то вместо t можно везде писать x n+ 1 и новая система не будет содержать явно время, но размерность вектора ее выходных координат увеличится на 1. В частном случае задачи с фиксированной конечной точкой x Т, но не фиксированным временем ее достижения Т, положив в выражении для Q G= 1, получим Q=T и требование Q=min превращается в T=min, то есть получаем задачу о максимальном быстродействии, сыгравшую большую роль в формировании общей теории оптимальных систем.
Дата добавления: 2015-07-25; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| О качественном анализе динамических систем | | | Динамическое программирование как математический метод решения задач оптимального управления |