Читайте также:
|
В математике существует понятие фазового портрета системы – под ним понимают совокупность траекторий решений, описывающих систему уравнений в n -мерном пространстве Rn – его называют фазовым пространством системы. Так как для пространств размерностью выше двух графическое отображение траекторий становится проблематичным, то реальное построение осуществляют на плоскости для сравнительно простых систем. Но само понятие фазовых траекторий оказывается полезным инструментом анализа динамики систем.
Рассмотрим для примера одномерную механическую систему, описываемую дифференциальным уравнением Ньютона для материальной точки:
m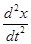 
=f (x).
Запишем его в виде системы двух уравнений первого порядка, введя новую переменную – импульс p=m 
и потенциальную энергию U (x) = – 
.
При этом возникает понятие гамильтониана (в нашем случае это просто полная энергия системы, но в других случаях это может быть значительно более сложное и глубокое понятие):
H (p, x) =U (x) +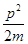 
и система может быть записана в виде
; 
.
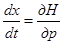Теперь можно рассмотреть плоскость (р, х), являющуюся фазовым пространством (но не являющуюся геометрическим пространством) – изображение движения системы будет более простым и понятным, хотя реально оно по-прежнему осуществляется вдоль единственной прямой.
Для простого гармонического осциллятора типа подвешенного на пружине груза полная энергия (гамильтониан):
H (p, x) = 
+ .
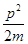Траектории на фазовой плоскости совпадают с линиями уровня гамильтониана
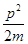+ =Е,
представляя собой семейства эллипсов 
= 1, где
a= 
b=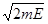 
.
В общем случае объекта, описываемого системой обыкновенных дифференциальных уравнений
=fi (t, x 1, …, xn, u 1, …, ur), i= 1, …, n
с начальными условиями t=t 0, xi (t 0) =xi 0 при выборе определенного допустимого управления u (t) движение объекта определено единственным образом и конец вектора x (t) опишет траекторию в пространстве своих координат. Эти координаты мы можем считать фазовыми координатами, а вектор x (t) будем называть фазовым вектором объекта,под которым будем подразумевать всякий вектор, компоненты которого полностью характеризуют текущее состояние объекта и при выбранном допустимом управлении и заданных начальных условиях полностью определяют движение объекта в рассматриваемые моменты времени.
В такой трактовке переходный процесс колебательного звена второго порядка может быть отображен на фазовой плоскости «функция решения – первая производная решения» и при затухающем переходном процессе годограф фазового вектора имеет вид спиралей, стягивающихся к началу координат или к эллипсам при гармонических воздействиях или нулевом затухании.
При выполнении компьютерного моделирования в лабораторных работах мы построим простейшие фазовые портреты управляемых объектов.
Дата добавления: 2015-07-25; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ограничения области применения. | | | О проблеме оптимального управления |