Производящая функция

Выше рассматривались испытания с одинаковыми вероятностями появления события; рассмотрим теперь испытания, в которых вероятности появления события различны. При решении задач на повторные независимые испытания, в которых вероятности появления событий различны, удобно пользоваться функцией вероятностей .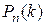

Пусть производится независимых испытаний, причем в первом испытании вероятность появления события равна 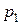, во втором – 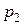,…, в -м – 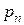; вероятности непоявления события соответственно равны .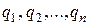

Производящей функцией вероятностей 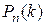называют функцию, определяемую равенством:

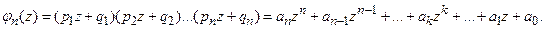
Вероятность 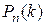того, что в независимых испытаниях событие появится ровно раз, равна коэффициенту при 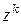в разложении производящей функции по степеням : .

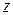Для проверки правильности вычисления производящей функции необходимо выполнение равенства

.

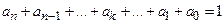Дата добавления: 2015-07-25