Читайте также:
|
Пусть производится 
независимых испытаний, в каждом из которых вероятность 
наступления события постоянна. Для определения вероятности 
используют формулу Бернулли. Если же велико, то пользуются асимптотической формулой Муавра-Лапласа. Однако эта формула непригодна, если вероятность события мала.
Итак, требуется найти вероятность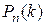 
при очень большом числе испытаний, в каждом из которых вероятность очень мала. Сделаем важное допущение: произведение 
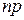сохраняет постоянное значение, т.е. 
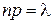. Это означает, что среднее число появлений события при различных значениях остается неизменным.
Теорема4. Если вероятность наступления события 
в каждом испытании стремится к нулю (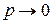
) при неограниченном увеличении числа испытаний (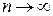
), причем произведение 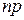стремится к постоянному числу 
(
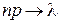), то вероятность 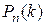того, что событие появится 
раз в независимых испытаниях, удовлетворяет предельному равенству
. (11)
Воспользуемся формулой Бернулли
.
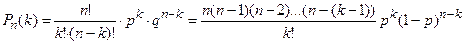Так как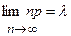 
, то при достаточно больших 
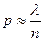и, следовательно,
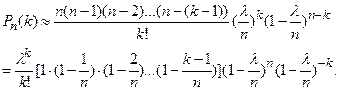
Учитывая, что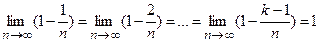 
, 
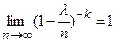и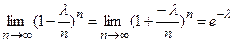 
, получим
.
Вообще говоря, условие теоремы Пуассона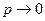 
при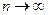 
, так что 
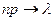, противоречит исходной предпосылке схем испытаний Бернулли (вероятность наступления события в каждом испытании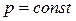 
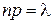). Однако, если вероятность – постоянна и мала, число испытаний – велико и число – незначительно (
), то из предельного равенства (11) вытекает приближенная формула Пуассона:
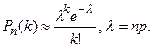(12)
Дата добавления: 2015-07-25; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В НЕЗАВИСИМЫХ ИСПЫТАНИЯХ | | | ПРОИЗВОДЯЩАЯ ФУНКЦИЯ |