Читайте также:
|
Легко видеть, что пользоваться формулой Бернулли при больших значениях 
достаточно трудно, так как при этом требуется выполнять громоздкие вычисления. Например, если 
, 
, 
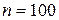, то 
.
Естественно требуется формула, отличная от формулы Бернулли, позволяющая хотя бы приближенно находить вероятность появления события ровно 
раз в независимых испытаниях, если число испытаний достаточно велико. Такой формулой является формула, устанавливаемая локальной теоремой Лапласа.
Заметим, что для частного случая, для 
, формула была найдена в 1730 г. Муавром; в 1738 г. Лаплас обобщил формулу Муавра для произвольного 
, 
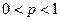. Поэтому теорему о которой далее пойдет речь, называют теоремой Муавра-Лапласа.
Теорема2. Если вероятность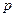 
наступления события 
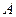в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 
того, что событие 
произойдет 
раз в 
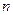независимых испытаниях приближенно равна (чем больше 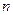, тем точнее) значению функции
при 
.
Итак, вероятность того, что событие появится в независимых испытаниях ровно раз, приближенно равна
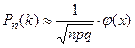при . (3)
Формула (3) носит название асимптотической формулы.
Для упрощения расчетов, связанных с применением формулы (3), составлена таблица значений функции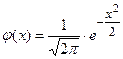 
– функции Гаусса (прил.1). При пользовании таблицей следует применять следующие свойства функции 
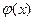: 1) функция 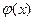четная, т.е. 
; 2) 
(на практике 
при 
).
Дата добавления: 2015-07-25; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ФОРМУЛА БЕРНУЛЛИ | | | ИНТЕГРАЛЬНАЯ ФОРМУЛА ЛАПЛАСА |