Читайте также:
|
На практике часто приходится сталкиваться со случаями, в которых требуется определить вероятность числа 
наступления некоторого события 
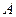в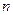 
испытаниях, например, вероятность числа бракованных изделий в данной партии.
Испытания, при которых вероятность появления события 
в каждом из них не зависит от исходов других испытаний, называют независимыми относительно события .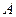
В разных независимых испытаниях событие может иметь либо различные вероятности, либо одну и туже вероятность. Будем далее рассматривать только такие независимые испытания, в которых событие имеет одинаковую вероятность.
Пусть производится 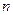независимых испытаний, в каждом из которых событие может появиться с вероятностью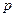 
. Тогда вероятность противоположного события (ненаступления события ) также постоянна в каждом испытании и равна 
.
Введем следующие обозначения: 
(или 
) – вероятность появления события в 
независимых испытаниях ровно раз; 
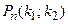– вероятность того, что событие появится в независимых испытаниях не менее 
и не более 
раз (кратко «от до раз»).
Вероятность того, что в независимых испытаниях событие наступит: менее раз, более раз, не менее раз, не более раз, не менее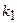 
и не более раз, – находят соответственно по формулам:
;
;
;
;
.
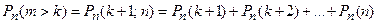Дата добавления: 2015-07-25; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Мысли и комментарии Тома. | | | ФОРМУЛА БЕРНУЛЛИ |