В независимых испытаниях

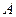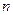Число наступления события в независимых испытаниях, в каждом из которых вероятность появления события постоянна и равна , называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях раз превышает (или по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.

Для нахождения решим следующую систему неравенств:

(9)

Рассмотрим первое неравенство системы (9). Используя формулу Бернулли, запишем:

.

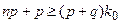После сокращений получим неравенство , откуда и или .

Решая аналогично второе неравенство системы (9), получим . Объединяя полученные решения двух неравенств, получим двойное неравенство

. (10)

При этом могут представиться следующие случаи:

а) если число 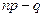– дробное, то существует одно наивероятнейшее число ;

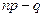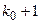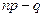б) если число – целое, то существуют два наивероятнейших числа, а именно: и ( и );

в) если число – целое, то наивероятнейшее число .

Дата добавления: 2015-07-25