
Читайте также:
|
Опять предположим, что в каждом из произведенных  испытаний событие
испытаний событие  появляется с одинаковой вероятностью
появляется с одинаковой вероятностью 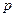 ,
, 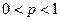 . Требуется вычислить вероятность
. Требуется вычислить вероятность 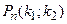 . В принципе каждое слагаемое можно вычислить по локальной формуле Муавра-Лапласа (3), но большое количество слагаемых делает расчет весьма громоздким. В таких случаях используется интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.
. В принципе каждое слагаемое можно вычислить по локальной формуле Муавра-Лапласа (3), но большое количество слагаемых делает расчет весьма громоздким. В таких случаях используется интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.
Теорема3. Если вероятность 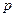 наступления события
наступления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 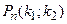 того, что событие
того, что событие  наступит в
наступит в  независимых испытаниях не менее
независимых испытаниях не менее 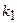 и не более
и не более 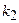 раз (включительно), приближенно равна определенному интегралу
раз (включительно), приближенно равна определенному интегралу
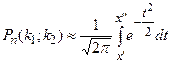 , (4)
, (4)
где 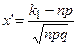 ,
, 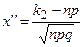 .
.
Преобразуем соотношение (4):
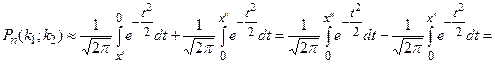
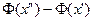 ,
,
где 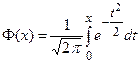 – функция Лапласа (или интеграл вероятностей).
– функция Лапласа (или интеграл вероятностей).
Итак, вероятность того, что событие 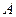 появится в
появится в 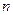 независимых испытаниях от
независимых испытаниях от 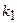 до
до 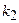 раз
раз
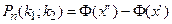 , (5)
, (5)
где 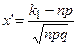 ,
, 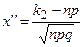 .
.
Функция 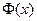 табулирована (см. прил. 2). При пользовании таблицей следует применять следующие свойства функции
табулирована (см. прил. 2). При пользовании таблицей следует применять следующие свойства функции 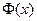 : 1) функция
: 1) функция 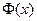 нечетная, т.е.
нечетная, т.е. 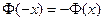 ; 2)
; 2) 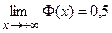 (на практике
(на практике 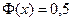 при
при  ).
).
Приведем следствие интегральной теоремы Лапласа.
Следствие. Если вероятность  наступления события
наступления события  в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе
в каждом испытании постоянна и отлична от нуля и единицы, то при достаточно большом числе 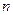 независимых испытаний вероятность того, что:
независимых испытаний вероятность того, что:
1) отклонение числа 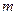 наступлений события
наступлений события  от произведения
от произведения  по абсолютной величине не более чем на заданную величину
по абсолютной величине не более чем на заданную величину 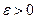
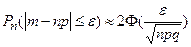 ; (6)
; (6)
2) относительная частота 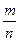 события
события  заключается в пределах от
заключается в пределах от 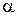 до
до 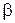
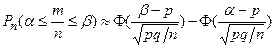 ; (7)
; (7)
3) отклонение относительной частоты 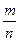 события
события  от постоянной вероятности
от постоянной вероятности  по абсолютной величине не более, чем на величину
по абсолютной величине не более, чем на величину 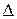
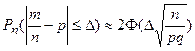 . (8).
. (8).
Доказательство. Докажем соотношение (6); (7) и (8) доказываются аналогично. Найдем вероятность осуществления неравенства 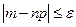 . Заменим это неравенство ему равносильным
. Заменим это неравенство ему равносильным
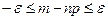 или
или 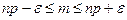 .
.
Поэтому по интегральной формуле Лапласа
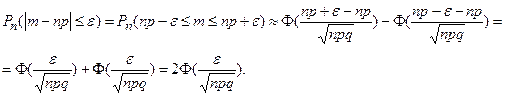
Дата добавления: 2015-07-25; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЛОКАЛЬНАЯ ФОРМУЛА МУАВРА-ЛАПЛАСА | | | В НЕЗАВИСИМЫХ ИСПЫТАНИЯХ |