Читайте также:
|
Пусть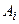 
и 
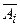– соответственно появление и непоявление события 
в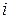 
-м испытании (
). 
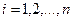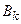– событие, состоящее в том, что в 
независимых испытаниях событие появится 
раз. Важно подчеркнуть, что не требуется, чтобы событие повторилось ровно раз в определенной последовательности. Воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.
Представим событие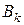 
через элементарные события 
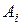. Например, при 
, 
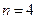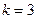событие
.
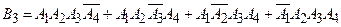В общем виде
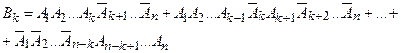(1)
Каждое слагаемое суммы (1) состоит из появлений события и 
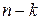непоявлений. Число всех слагаемых равно числу способов выбора из испытаний , в которых событие произошло, т.е. числу сочетаний 
. Вероятность каждого такого слагаемого по теореме умножения для независимых событий равна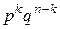 
, а так как слагаемые события между собой несовместны, то по теореме сложения вероятностей несовместных событий получим
.
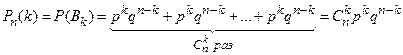Итак, мы доказали следующую теорему.
Теорема1. Если вероятность 
наступления события в каждом испытании постоянна, то вероятность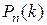 
того, что событие наступит раз в независимых испытаниях, равна
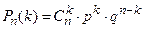или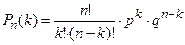 
(
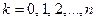). (2)
Формулу (2) называют формулой Бернулли.
Дата добавления: 2015-07-25; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СХЕМА НЕЗАВИСИМЫХ ИСПЫТАНИЙ | | | ЛОКАЛЬНАЯ ФОРМУЛА МУАВРА-ЛАПЛАСА |