Критический анализ основных понятий

1.2.1. Атомные и молекулярные орбитали (АО и МО). Не следует забывать, что строгое решение квантовомеханического уравнения Шрёдингера возможно только для водородоподобного атома, а АО и МО многоэлектронных систем - это результат использования одноэлектронного приближения. Строгий физический смысл имеют только полная энергия системы и полная электронная плотность в точке, а их разбиение на одноэлектронные (орбитальные) вклады - лишь условно, хотя и очень полезно. Наряду с методами молекулярных орбиталей и валентных связей (ММО и МВС), широко используемыми в учебной литературе, в профессиональных квантовохимических расчётах всё шире и успешнее используется теория функционала электронной плотности (DFT), где вовсе нет отдельных орбиталей. Однако здесь она не рассматривается из-за отсутствия простой качественной модели.

1.2.2. Координационное число (КЧ) и координация. Атомы в простых и сложных веществах располагаются друг относительно друга определенным образом, это расположение можно объективно установить на опыте, даже не понимая природы химической связи. И в данном пособии мы будем преимущественно исходить не из теорий химической связи (все они имеют приближённый характер), а из обобщения экспериментальных данных о строении.

КЧ атома - это число его ближайших соседей. В этом определении нет слова “связь”, но оно подразумевается: если атомы все время удерживаются на коротком расстоянии - очевидно, существует связь, электронные оболочки взаимодействуют. И наоборот, если расстояние очень велико, то взаимодействием можно пренебречь. Понятие КЧ применимо к любым веществам, а не только к так называемым “координационным соединениям” (этот термин лишь создаёт путаницу), и к атомам любых элементов. Если структура расшифрована, то, казалось бы, координационное число определено однозначно и спорить тут не о чем. Например, в молекуле NaCl (газ.) каждый ион имеет КЧ 1, а в кристалле NaCl - КЧ 6. Но правила подсчета соседей далеко не всегда ясны и однозначны.

Если на разном удалении находятся атомы разного сорта, то более далёкие соседи не обязательно связаны слабее. Рассмотрим ту же структуру типа NaCl, которую имеют многие монооксиды, нитриды, переходных металлов. Там каждый ион имеет шесть соседних ионов противоположного знака на одинаковых расстояниях, а следующие по дальности соседи - с седьмого по восемнадцатый - являются ионами того же знака и расположены на гораздо большем расстоянии (в Ö2 раз больше кратчайшего), поэтому вроде бы ясно, что КЧ равно 6. Однако, строго говоря, для оценки прочности связи расстояния А-Х, А-А и Х-Х нужно сравнивать не друг с другом, а с такими же расстояниями в тех веществах, для которых имеются сведения о прочности связи или с суммами соответствующих радиусов (см. п. 1.2.9). В данном случае можно сравнить расстояния в оксиде с расстояниями в соответствующих простых веществах (табл. 2).

Таблица 2. Межатомные расстояния в некоторых оксидах МО типа NaCl

и в соответствующих простых веществах

М	Расстояние, Å	Вывод о связях М-М в оксиде
М-О	М-М
	в оксиде	в металле
Са	2,40	3,39	3,94	нет, т.к. нет электронов для этого
Ti	2,12	3,00	2,96	есть, т.к. есть электроны, и расстояние позволяет
Ni	2,09	2,96	2,49	нет, т.к. расстояние большое

Нормальная длина связи О-О находится в пределах 1,1-1,5 Å (см. табл. 4). Поэтому расстояния О-О в оксидах (они такие же, как расстояния М-М), можно уверенно считать несвязевыми. Не так однозначна ситуация с расстояниями М-М. В оксиде никеля расстояние М-М заметно длиннее, чем в простом веществе, поэтому можно считать, что связи нет, и d-электроны локализованы на ионе никеля, что подтверждается его окраской и низкой электропроводностью. В случае титана расстояния в оксиде и в металле примерно равны, а в случае кальция расстояние в оксиде даже короче, чем в металле (при поглощении кальцием кислорода объем твердой фазы уменьшается!). Значит ли это, что там есть связи металл-металл? Часто отвечают - да. Но есть ли электроны для этой связи? В оксиде титана - есть, т.к. титан - элемент 4-группы, и в степени окисления 2 у него остается 2 валентных электрона. В оксиде кальция - нет, т.к. все валентные электроны кальция израсходованы на связь с кислородом. В соответствии с этим, TiO имеет металлическую проводимость, а CaO - диэлектрик.

Выводы: во всех трех оксидах КЧ обоих компонентов равно шести (октаэдрическое окружение), кроме Ti, окружение которого в TiO более сложное: 6О + 12Ti.

Многие немолекулярные вещества нестехиометричны, имеют дефектную структуру, где не все идеальные позиции заселены (или, наоборот, имеются дополнительные атомы в необычных местах). Типичными примерами являются рассмотренные выше оксиды титана и никеля. В такой структуре фактические КЧ некоторых атомов отличаются от идеальных. Например, если есть вакансии катионов, то у некоторых анионов будет КЧ 5, а не 6.

Иногда (довольно редко) встречается сильно асимметричное окружение с большим числом неравноценных расстояний, где трудно провести границу между ближайшими и дальними соседями. Рассмотрим три примера (табл.3). В оксидах титана и хрома граница между короткими и длинными расстояниями видна хорошо: связи отличаются по длине всего на 0,03-0,16 Å, а следующее за ними расстояние отличается на 1,3-1,5 Å, т.е. превышает кратчайшее в 1,8-1,9 раза. КЧ катионов равны соответственно 6 и 4 и сомнений не вызывают. Но в структуре V₂О₅ длины связей сильно отличаются (причины такой асимметрии обсуждаются в модуле 4). Сколько соседей считать ближайшими? Ответ неоднозначен. Наиболее сильные различия наблюдаются между пятым и шестым, шестым и седьмым расстояниями. Поэтому иногда указывают КЧ 5, иногда 6. Для более объективной оценки относительной прочности связей можно рассчитать и сравнить валентности связи (см. модуль 3). Но какую бы цифру КЧ мы не назвали, она не даст ясного представления о сути дела. Нужно не ограничиваться одной цифрой, а описать всё окружение.

Таблица 3. Расстояния металл-кислород (Å) в структурах высших оксидов титана, ванадия и хрома, перечисленные в порядке возрастания (до девятого соседа включительно)

сосед
TiO2	1,95	1,95	1,95	1,95	1,98	1,98	3,49	3,49	3,49
V2O5	1,56	1,75	1,76	1,84	2,03	2,83	3,41	3,59	3,61
CrO3	1,60	1,60	1,76	1,76	3,10	3,34	3,39	3,39	3,40

В некоторых структурах, в частности, в p-комплексах металлов с непредельными и ароматическими молекулами, в качестве соседей иногда рассматривают не отдельные атомы, а целые атомные группы или даже электронные пары. Например, в качестве КЧ железа в “сэндвичевой” молекуле ферроцена Fe(C₅H₅)₂ иногда указывают 10 (по числу атомов С, одинаково близких к атому Fe), иногда 2 (по числу циклопентадиенильных анионов, ведь атомы углерода связаны друг с другом и подходят к атому железа не поодиночке, а группами по 5), а иногда 6 (по числу p-электронных пар).

Таким образом, понятие КЧ не очень чёткое:

- оно не показывает природу соседей (а ведь они могут быть атомами разных элементов, или атомами одного элемента, но имеющими разное окружение);

- при одном и том же КЧ возможны разные формы окружения;

- при однотипной форме окружения возможны разные расстояния и валентные углы.

Все эти неясности устраняются, если вместо указания одной цифры КЧ - охарактеризовать координацию полностью. Координация данного атома - это число, вид и расположение его соседей. Атом с его ближайшими соседями будем называть координационной группой (см. п. 1.3). Координация - важнейшее понятие структурной химии, поддающееся объективному определению. Наша задача - научиться описывать её, а затем и прогнозировать на основе некоторых общих (хотя и не вполне чётких) структурных принципов.

1.2.3. Химическая связь. Существование химических связей объективно проявляется в том, что в большинстве веществ (кроме благородных газов) при невысоких температурах атомы существуют не поодиночке, а в виде устойчивых групп из двух или более атомов, находящихся на малых и приблизительно постоянных расстояниях. Если бы ничто не удерживало атомы, они бы разлетались в результате теплового движения в разные концы колбы (или в разные концы Вселенной). Атомы соединяются самопроизвольно, а для того, чтобы их разъединить, разорвать связь, нужно затратить энергию.

Механизм любой химической связи в самом общем виде состоит в том, что при сближении атомов изменяются их квантовые состояния, перераспределяется в пространстве электронная плотность, и энергия электростатического взаимодействия всех ядер и всех электронов становится ниже, чем была в обособленных атомах. С точки зрения квантовохимических расчётов, все связи имеют по сути единую природу, и классификация на разные типы не нужна. Но упрощённые качественные модели связи применимы лишь к отдельным классам веществ.

1.2.4. Предлагаемая классификация веществ по характеру связи основана лишь на применимости или неприменимости тех или иных упрощённых подходов и не имеет глубокого теоретического обоснования. Ниже в число химических связей не включены водородная связь и силы Ван дер Ваальса, поскольку они обычно гораздо слабее перечисленных связей. Это также несколько произвольно, поскольку между водородной и ковалентной связью нет принципиального отличия, и есть по крайней мере одна структура (ион HF₂^-), где они неразличимы.

Классические ковалентные структуры -структуры, которые можно описать с помощью классического представления о валентности (см. модуль 2), т.е. о парноэлектронных двухцентровых связях. Как показывает опыт, они должны удовлетворять одновременно двум условиям:

а) соединяющиеся атомы должны иметь высокую электроотрицательность (ЭО), проще говоря - быть атомами неметаллов;

б) суммарное число электронов на их внешних уровнях должно быть равно суммарному числу орбиталей на их внешних уровнях или превосходить его.

Если эти условия выполняются, то почти все возможные структуры (а значит и составы!) веществ вытекают из простого правила: число связей (валентных штрихов), сходящихся на атоме, должно быть равно его валентности. Типичные примеры - углеводороды, спирты, оксиды и кислородные кислоты фосфора, серы, хлора и т.п. Подробнее см. в модуле 2.

Неклассические ковалентные структуры -структуры, удовлетворяющие условию а, но нарушающие условие б. С точки зрения метода МО они ничем принципиальным не отличаются от классических структур, но для них уже не удаётся нарисовать традиционные валентные схемы, где число связей, сходящихся на данном атоме, определяется его валентностью. Таким образом, валентность не позволяет прогнозировать их структуры. Типичные примеры - бороводороды, где “трёхвалентный” атом бора имеет КЧ 4, 5 или 6, а “одновалентный” водород часто имеет КЧ 2, и металлические кластеры. Понятие “степень окисления” (п. 1.2.5) здесь тоже бесполезно из-за малой полярности связей.

Металлические структуры -структуры, построенные только из атомов с близкой и невысокой ЭО (т.е. атомов металлов и, может быть, близких к ним по ЭО неметаллов). Их составы и КЧ тоже нельзя предсказать на основе валентности или степени окисления. Отличие от неклассических ковалентных структур лишь в том, что в металлах электроны делокализованы не между несколькими атомами (2-100), а между всеми атомами данного куска (более 10¹⁰). По мере роста металлических кластеров они постепенно становятся из молекул кусочками металла.

Ионные структуры -структуры, построенные из противоположно заряженных одноатомных частиц - ионов. Обычно для образования ионной связи требуется взаимодействие атомов с большой разницей ЭО (более 2, см. Приложение 1), то есть металлических и неметаллических элементов. В этом случае традиционное понятие валентности не позволяет правильно прогнозировать КЧ, но зато приобретает смысл понятие “степень окисления” (п. 1.2.5), позволяющее предсказывать если не структуры, то хотя бы составы соединений на основе условия электронейтральности. Иногда говорят, что ионная связь - это разновидность полярной ковалентной связи, и рассматривают её на примере двухатомных молекул (LiH, LiF и т.п.). Такие молекулы действительно ничем принципиальным не отличаются от НF или NO. Но реальные фториды и гидриды щелочных металлов в обычных условиях устроены совсем не так. Там нет отдельных двухатомных молекул, у каждого атома - 6 соседей. Описывать это методами ВС или МО очень неудобно. Строение таких веществ можно эффективно описать ионной моделью (см. модуль 3), даже если прямых доказательств существования ионов для данного вещества нет.

Структуры с промежуточными типами связи и структуры, где совмещаются разные типы связей. Именно такие структуры и составляют большинство неорганических веществ. Но следует понимать, что это два разных случая. Например, структуру ZnS можно рассматривать и как ионную, и как построенную на ковалентных донорно-акцепторных связях. Характер связи здесь промежуточный между ионным и ковалентным, но все связи одинаковые - структура гомодесмичная. А в структуре ацетата натрия сочетаются классические ковалентные связи С-Н, С-С, С-О внутри ацетат-ионов и типичные ионные связи О-Na. Это пример гетеродесмичной структуры. Туда же относятся соединения, содержащие сложные катионы с ковалентными связями, простейшим примером которых является ион аммония NH₄⁺. Следовательно, ионная связь возможна и в соединениях, не содержащих элементов с низкой ЭО - металлов, (например, в ацетате аммония), но в таких веществах не она является наиболее прочной связью.

1.2.5. Понятия “валентность” и “степень окисления” часто смешивают, что приводит к ошибкам, тем более, что понятие “валентность” имеет множество противоречивых и нечётких определений.

Классическое определение “валентность - свойство атома присоединять или замещать определенное число атомов другого элемента” возникло в эпоху, когда экспериментальных данных о структуре почти не было, и в нём спутаны состав и структура. Например, в хлориде натрия каждый атом хлора присоединяет к себе один атом натрия, если описывать состав, и шесть атомов натрия, если описывать структуру. Что же называть его валентностью? Обычно отвечают - единицу, то есть игнорируют структуру, а опираются на состав. Но тогда, если быть последовательным, нужно считать, что валентность углерода в ацетилене и бензоле - не 4, а тоже 1, потому что простейшая формула СН. Отсюда видна бессмысленность такого понятия. Если Вас спросят, какова валентность хлора в NaCl - отвечайте, что его КЧ 6, а степень окисления минус 1.

Несколько лучше определение валентности, как числа электронов, используемых атомом для образования связи. Теперь видна разница между натрием и углеродом. Такое понятие валентности фактически используется ниже при определении порядка связи или валентности связи (п. 1.2.7). Но остаётся непонятным, можно ли с помощью этой величины прогнозировать КЧ или только состав вещества, как учесть возможность донорно-акцепторных связей и т.д. Если, например, и натрий, и водород одновалентны, то почему в своих хлоридах они имеют столь различные КЧ - 1 и 6?

В физической литературе иногда употребляют валентность в смысле “число электронов на внешнем уровне”. Тогда у кислорода она равна шести, а у палладия - нулю или 18 (4s²4p⁶4d¹⁰5s⁰). Это вносит ещё большую путаницу.

В данном пособии предлагается различать валентность и степень окисления и применять их лишь в определённых, заранее оговоренных случаях. Ценность этих величин в том, что они могут быть определены до эксперимента и далее могут в известных случаях использоваться для прогноза состава, межъядерных расстояний, координации, прочности связей и др. Рекомендуемое определение валентности см. в модуле 2.

Степень окисления - это формальный заряд атома, вычисленный в предположении, что все образованные им полярные связи являются ионными, то есть валентные электроны полностью перешли к атомам с большей ЭО. Это понятие стоит применять только там, где соседние атомы сильно отличаются по ЭО, то есть при ионной или полярной ковалентной связи. Для элементарных ионов она имеет реальный физический смысл - заряд иона, при полярной ковалентной связи это условная, но полезная величина. Можно описать строение и свойства веществ, в том числе окислительно-восстановительные реакции, не используя этого понятия, но с ним удобнее.

Степени окисления можно прогнозировать по положению элементов в периодической системе, а по степеням окисления можно прогнозировать составы, но не структуры веществ. Если степень окисления бария 2, а хлора минус 1, то состав хлорида бария BaCl₂, а не BaCl или BaCl₃ (условие электронейтральности!), но отсюда никак не следует, что в его структуре вокруг иона бария - два иона хлорида. Их гораздо больше, т.е. КЧ вовсе не обязательно равно степени окисления. Но введение степеней окисления всё же облегчает прогноз структуры: каждой степени окисления соответствует свой ионный радиус и своя электронная формула, что учитывается при прогнозе координации.

Наоборот, проверяя заданный состав по степеням окисления, можно обнаружить гомоатомные связи. Если состав вещества ВаО₂, а степень окисления бария не может быть 4, значит степень окисления кислорода минус 1 вместо нормальной минус 2, значит ещё один электрон атом кислорода тратит на связь с другим атомом кислорода, значит в структуре есть группировки О₂^2-.

Если соединяются элементы с близкими электроотрицательностями (металл с металлом, углерод с водородом, железом или бором и т.п.), то степени окисления обычно бесполезны для прогноза состава и тем более структуры.

1.2.6. Энергия связи. Это наиболее прямая характеристика прочности химической связи - энергия, необходимая для разрыва связи. Но ее редко можно объективно определить. Помимо экспериментальных трудностей, существует принципиальное возражение: нельзя разорвать одну связь в сложной структуре, не изменив остальных связей. Например, для последовательного отрыва четырех атомов водорода от молекулы метана требуются разные энергии: 426, 368, 518 и 334 кДж/моль. Но это не значит, что связи неравноценны, просто второй атом водорода отрывается уже не от молекулы метана, а от метильного радикала. Если бы энергии связей и в самом деле имели эти неодинаковые значения, то легче всего отрывался бы четвертый атом. Объективному определению поддаётся энергия атомизации - энергия, необходимая для разрыва всех связей - разрушения сложной структуры на отдельные невзаимодействующие (газообразные) атомы. Поскольку в молекуле метана все 4 связи одинаковы по длине, и валентные углы тоже одинаковы, то за энергию одной связи можно принять среднее значение энергии разрыва связи, то есть 1/4 энергии атомизации: 412 кДж/моль. Но если связи неравноценны (например, в молекуле этана или НСN), то ясно, что поровну делить нельзя, но как разделить - неясно. Предложены разные подходы, но все они нестрогие. Поэтому, если иногда приводят энергию отдельной связи в сложной структуре с точностью 4-5 значащих цифр, - это говорит о плохом понимании сути дела. Там имеют смысл не более двух цифр. Иногда в качестве меры прочности связи в веществе приводят изменение энтальпии DH (или энергии Гиббса DG) образования вещества. Это неверно, т.к. в исходных простых веществах тоже есть довольно прочные связи. Поэтому DH атомизации сложного вещества - это разность DH атомизации простых веществ и DH образования из них сложного вещества. DH и DG атомизации простых веществ известны [5]. Зная это и DH образования сложного вещества, всегда можно вычислить его DH атомизации, которая и будет объективной мерой прочности связей в веществе. Но она характеризует все связи вместе, а не каждую по отдельности. Энергия решётки используется для оценки прочности связи в кристаллическом веществе. Это не очень удачный термин, поскольку решётка - это чисто геометрическое понятие, не несущее химического смысла. Энергия решётки - это энергия, необходимая для разложения кристалла на отдельные невзаимодействующие (газообразные) составные части. Она зависит от того, что принято за составные части. Если атомы - она совпадает с энергией атомизации, если ионы или молекулы - это совсем другая величина. Например, энергия ионной решётки хлорида натрия - это энергия, необходимая для превращения кристалла в газообразные ионы, а не атомы, хотя такой процесс реально неосуществим. Она удобна, когда нужно сравнить разные варианты ионных структур из одних и тех же ионов, но если нужно сравнивать вещества с разным характером связи, то полезнее энергия атомизации.

1.2.7. Порядок связи. Валентность связи. Поскольку химическая связь образуется в результате перераспределения электронной плотности, то при прочих равных условиях она тем прочнее, чем больше электронов в ней участвует (точнее - чем больше электронов на связывающих МО и чем меньше электронов на разрыхляющих МО). Это позволяет ввести электронные критерии прочности связи, которые можно оценивать до опыта. Для структур с ковалентной связью такой критерий - это порядок связи (или кратность связи), который оценивается методами МО или ВС, особенно просто - для классических ковалентных структур (подробнее см. модуль 2).

Для ионных и ионно-ковалентных структур (всех тех, где можно определить степень окисления) весьма полезный критерий - валентность связи. Это по сути тот же порядок связи, но для случая, когда КЧ больше степени окисления (формальной валентности), когда нельзя нарисовать валентную схему, поскольку порядок связи меньше единицы (подробнее см. п. 3.2).

Оба эти понятия нестрогие, но полезные для качественного сравнения энергий связи и количественного прогноза их длин.

1.2.8. Длина связи - это очень удобная и наглядная, хотя и не количественная, мера прочности связи между двумя данными атомами - равновесное межъядерное расстояние. Главное достоинство: это расстояние измеряется без разрыва связи, и сразу для всех связей. Точность современных структурных методов достаточно высока, и ограничением обычно является тепловое движение атомов (амплитуда тепловых колебаний во много раз больше погрешности измерения, и для получения наиболее точных значений желательно охлаждать вещество). Когда говорят о межатомном расстоянии, всегда имеется в виду расстояние между ядрами, т.к. ядро - это единственная часть атома, положение которой можно точно определить.

Если какие-то два атома находятся на большом расстоянии - можно считать, что связи между ними практически нет, т.к. электронные оболочки не перекрываются. Если они сильно сближены - то, очевидно, это энергетически выгодно, т.е. образовалась связь. Здесь, конечно, подразумевается самопроизвольное сближение: ведь при высоком внешнем давлении атомы сближаются вынужденно, и при этом энергия системы не понижается, т.е. связь не упрочняется. Встречаются, хотя и редко, случаи, когда атомы вынуждены сближаться на аномально короткое расстояние под влиянием соседей, без внешнего воздействия. При внимательном анализе это обычно можно выявить.

Но что значит "большое и маленькое расстояния"? Где граница между ними? Примеры, приведённые в табл. 4 (а также в табл. 3), показывают, что между короткими “связевыми” и длинными ”несвязевыми” расстояниями иногда существует объективная граница, не зависящая от наших мнений: промежуточные расстояния просто не встречаются. Конечно, так бывает не у всех элементов (особенно при ионной связи, которая имеет дальнодействующую природу), и часто такое деление соседей на “связанные” и “несвязанные” является условным (п. 1.2.2).

Таблица 4. Расстояния О-О и Si-O в известных структурах (несколько сотен веществ, несколько тысяч коротких расстояний и ещё больше длинных)

Диапазон расстояний, Å	Распространенность таких расстояний	Комментарий
О-О	Si-O
менее 1,1	менее 1,5	не встречаются никогда	отталкивание заполненных внутренних оболочек
1,2-1,5	1,55-2,0	встречаются очень часто	химическая связь
1,6-2,0	2,1-2,9	не встречаются никогда	отталкивание заполненных внешних оболочек
более 2,1	более 3,0	встречаются очень часто	нет ни связи, ни сильного отталкивания

1.2.9. Атомные и ионные радиусы. Размер атомов и ионов определяется их электронными оболочками. Но из-за волновых свойств электронов точный радиус этих оболочек определить невозможно: на большом удалении от ядра электронная плотность убывает, но в ноль, строго говоря, не обращается. Кроме того, при наличии связей оболочки не могут быть сферическими: в направлении связи и в несвязевом направлении электронная плотность изменяется по-разному. Таким образом, атомные и ионные радиусы не могут иметь строгого смысла. Но с другой стороны, при образовании связей атомы все же сближаются на более или менее определённые расстояния (см., например, табл. 3, 5), и связи с серой всегда длиннее связей того же элемента с кислородом. Поэтому с практической точки зрения можно и нужно уметь оценивать и сравнивать атомные размеры, не забывая об их условности.

В структурной химии радиусы обычно определяют по опытным данным на основе модели жёстких сфер. Структура рассматривается как совокупность соприкасающихся шаров, тогда длина связи (т.е. та величина, которая может быть определена объективно) равна сумме радиусов. Это и есть определение радиуса: атомные и ионные радиусы - это величины, подобранные таким образом, чтобы их суммирование давало правильные межъядерные расстояния. Другого, более глубокого, смысла искать не следует, ведь на самом деле при образовании связи оболочки деформируются и перекрываются, а не касаются. Но при всей примитивности модели жёстких сфер она даёт удивительно хорошие результаты.

Ковалентная, металлическая связь и вандерваальсово взаимодействие возможны как между одинаковыми, так и между разными атомами. Поэтому ковалентный радиус атома Х определяют как половину длины ординарной связи Х-Х. Аналогично вандерваальсов радиус атома Х - это половина расстояния между сближенными атомами Х, принадлежащими разным молекулам (т.е. ковалентно не связанными), а металлический радиус атома А - это половина межъядерного расстояния А-А в металлическом простом веществе (обычно его указывают для КЧ 12, как наиболее типичного). Ковалентные и металлические радиусы собраны в Приложении 4 задачника [2]. Естественно, вандерваальсов радиус атома значительно больше ковалентного. Ковалентные радиусы рекомендуется использовать только для ординарных связей, а для кратных лучше применять кривые порядок связи-длина связи (см. модуль 2).

В отличие от случаев, рассмотренных выше, ионный радиус нельзя определить как половину межъядерного расстояния, так как касаются разные ионы. Чтобы найти радиус одного из них, нужно знать радиус другого. Поэтому радиус одного иона оценивают с помощью каких-то дополнительных методов [6, 11, 12], и, в зависимости от метода, получают разные результаты, а потом на его основе строят систему радиусов. Наиболее подробная сводка ионных радиусов дана Шенноном в 1976 г. Взяв за основу традиционное значение радиуса аниона кислорода 1,40 Å, и вычитая его из расстояний в кислородных соединениях, он получил набор радиусов катионов. Затем, вычитая эти радиусы из длин связей в хлоридах, получил много разных, но близких значений радиуса хлорид-иона и усреднил их. Аналогично - с остальными анионами. Тот же автор привёл доводы в пользу уменьшения радиуса кислорода до 1,26 Å и на основе этой величины получил вторую систему радиусов. Естественно, в ней радиусы всех катионов на 0,14 Å больше, а анионов - на 0,14 Å меньше, чем в первой системе. Эта вторая система приведена в Приложении 2 задачника [2]. Какая из них правильнее? Однозначного ответа не может быть. Длины связей они прогнозируют совершенно одинаково (не надо только складывать радиусы, взятые из разных систем!). Для прогноза координации считается лучше вторая. Но некоторые расстояния между одноимёнными ионами противоречат обеим системам. Так, несвязевые расстояния О-О бывают и меньше 2,8 Å (см. табл. 4), что противоречит первой системе и требует перехода ко второй. Но этому препятствует существование соединений с расстояниями К-К короче 2,9 Å.

Атомные и ионные радиусы зависят от координации: чем больше соседей, тем сильнее их отталкивание, тем больше длина связи, а мы называем это увеличением радиуса центрального атома. Иногда применяются процентные поправки, например, у металлов для перехода от КЧ 12 к КЧ 8 рекомендуется уменьшить радиус на 2%. В системе Шеннона радиусы для каждой координации определены независимо: по тем соединениям, где реально имеется такая координация.

Если катион 3d-элемента может находиться как в высокоспиновом, так и в низкоспиновом состоянии (см. модуль 4), то его радиус в высокоспиновом состоянии заметно больше, так как заселены орбитали, расположенные близко к лигандам и отталкивающие их. Это также учтено в системах Шеннона.

Радиусы очевидным образом зависят от степени окисления: чем меньше электронов, тем меньше размер, особенно если при отдаче электронов уменьшается главное квантовое число внешнего уровня. Зависимость радиусов от природы элемента даётся Периодическим законом.

Для пользования ионными радиусами вовсе не обязательно, чтобы связь была чисто ионной. Достаточно такого различия в ЭО, чтобы атомам можно было уверенно приписать степени окисления. Например, связи S-O, S-F, S-Cl - это классические ковалентные связи, иона S⁶⁺ нет. Но его шенноновский радиус в сумме с радиусами анионов кислорода, фтора, хлора даёт близкие к действительности длины связей (ведь именно из таких длин связей он и вычислен!).

Если учтены все приведённые выше оговорки, то суммирование радиусов, определённых по экспериментальным данным для одних веществ с металлической, ионной или ионно-ковалентной связью, даёт правильный прогноз средних расстояний в других веществах с точностью не хуже 5 % (обычно - не хуже 2%). Но следует подчеркнуть слово средних. Связи в координационной группе могут быть неравноценны, и отдельные расстояния могут отличаться от среднего на 10-20 %. С помощью радиусов предсказать такую неравноценность нельзя, нужны другие подходы (см. модули 3, 4).

Слэтер предложил единую систему атомных радиусов для всех типов связи. Действительно, хотя радиусы катионов существенно меньше соответствующих металлических радиусов, зато радиусы анионов намного больше ковалентных радиусов соответствующих неметаллов. Поэтому сумма металлического радиуса А и ковалентного радиуса Х близка к сумме ионных радиусов А⁺ и Х^-. Но всё же погрешность прогнозов по слэтеровским радиусам гораздо больше - до 15%, и нет смысла пользоваться ими при наличии более совершенных систем. К тому же сильное различие в размерах между атомами и ионами подтверждается экспериментально - данными рентгеноструктурного анализа о распределении электронной плотности и тем, что в оксидах, фторидах и гидридах щелочных и щелочноземельных металлов расстояние между катионами существенно меньше суммы атомных радиусов (см. пример СаО в табл. 2).

До сих пор шла речь об эмпирических радиусах (основанных на экспериментально измеренных расстояниях). Кроме того, путём квантовохимических расчётов получают орбитальный радиус. Это расстояние от ядра до главного максимума электронной плотности последней занятой орбитали атома. Точность расчётов может быть высокой, но сумма орбитальных радиусов - это ещё не длина связи, поэтому далее они не рассматриваются.

Таким образом, абсолютные значения радиусов (особенно ионных) точно неизвестны, и всякая используемая величина имеет смысл лишь в рамках определённой системы. Если в учебнике или справочнике приводятся радиусы без указания характера связи, автора системы, координации, спинового состояния (или, хуже того, вперемешку даны разнородные радиусы), это говорит о плохом понимании сути дела, но, к сожалению, встречается часто.

1.2.10. Понятие " молекула ". Определение молекулы как мельчайшей частицы вещества, сохраняющей его химические свойства, безнадёжно устарело. Во-первых, одна молекула не дает никакого представления о химических равновесиях, механизмах реакций, термодинамических свойствах. Чему равна константа диссоциации или степень диссоциации одной молекулы? Как записать уравнение диссоциации воды без помощи второй молекулы, сольватирующей протон? Какая молекула: NO₂ или N₂O₄ - сохраняет свойства оксида азота (4)? Во-вторых, у многих веществ эта частица неопределенно велика. Согласно этому определению, кусок аморфного кремнезема или кварца есть молекула, но тут возникает трудный вопрос о наименьшем кусочке, который еще сохраняет свойства вещества.

Иногда молекулой называют любую химическую структуру, в том числе частицу H₂O, кристалл, кусок стекла. Но такой термин не нужен, т.к. равносилен понятию "вещество". Заряженные и незаряженные, микроскопические и макроскопические тела желательно различать.

Кинетическое определение молекулы. Стоит задуматься: а откуда вообще узнали о существовании молекул? Из молекулярно-кинетических явлений в газах и жидкостях. Фактически под молекулой, как объектом молекулярно-кинетической теории, подразумевается всегда электронейтральная частица, способная к тепловому движению отдельно от других частиц. Если молекулы не движутся, то очень трудно экспериментально доказать, что они существуют. Все экспериментальные способы определения молекулярных масс (по плотности паров, осмотическому давлению растворов, масс-спектрам, понижению давления пара или температуры замерзания, повышению температуры кипения) основаны на движении частиц. Задача нахождения молекулярной массы кварца или стекла не имеет решения. Эти вещества можно перевести в раствор или в пар только ценой полной потери их химической индивидуальности (например, при растворении в HF). Ниже даны ещё два определения молекулы, но они всё же являются косвенными и позволяют не измерить, а лишь рассчитать молекулярную массу. К тому же под эти определения не подпадают одноатомные молекулы.

Энергетическое определение молекулы. По предыдущему определению существование молекул очевидно лишь в газовой фазе. Для конденсированных (жидких и твёрдых) фаз предложено следующее определение. Молекула в конденсированной фазе существует, если для отрыва её (перевода в газовую фазу) требуется гораздо меньшая энергия, чем для отрыва любой её части. Например, энтальпия испарения одной молекулы Н₂О из кристалла льда равна 7´10^-20 Дж, а энтальпия отрыва одного атома водорода - 8´10^-19 Дж, то есть на порядок больше. Это значит, что связи между группировками Н₂О гораздо слабее связей внутри группировок, и позволяет считать эти группировки молекулами. Вода здесь взята как пример молекулы с особенно прочными межмолекулярными водородными связями. У малополярных и неполярных молекул энергия межмолекулярного притяжения ещё меньше: например, у Н₂ - на два порядка меньше энергии ковалентной связи. Однако сложная молекула (например, сахара или белка) может образовать с соседними молекулами так много водородных связей, что их суммарная энергия окажется больше энергии одной ковалентной связи, и по данному определению получится, что молекул нет.

Как показано в п. 1.2.8, суждения о наличии и прочности связей можно строить на основе межатомных расстояний, не разрывая связей. Отсюда геометрическое определение молекулы - на основе данных рентгеноструктурного анализа кристалла. Молекула - это такая конечная группа атомов, в которой каждый атом имеет на расстоянии, соответствующем связи, хотя бы один атом из той же группы и ни одного атома, не входящего в неё. Правда, такое определение не отличает молекулу от сложного иона, но в этом обычно можно разобраться.

1.2.11. Немолекулярные вещества. Это понятие отрицательное. Нет молекул, а что же есть? Иногда отвечают: есть атомы. Но если атомы не связаны друг с другом (как у благородных газов), то их надо считать одноатомными молекулами. А если связаны - надо это указать. Если и аргон, и углерод записывают, как одиночные атомы, то почему у первого энергия атомизации равна нулю, а у второго она самая большая из всех "простых" веществ? Немолекулярными веществами называют те, где прочными связями соединено вместе настолько большое число атомов, что эта группировка уже не обладает свойствами молекулы, указанными в п. 1.2.10. Иными словами, система прочных связей практически бесконечна. Простейшим и важнейшим примером является диоксид кремния. В отличие от своего аналога углерода, кремний в диоксиде образует не две двойных связи, а четыре простых с четырьмя разными атомами кислорода. Эта группа SiO₄ не является молекулой, поскольку каждый атом О связан ещё с одним атомом Si, тот - ещё с тремя атомами О и так далее до края кристалла или куска стекла.

Где граница между молекулярными и немолекулярными веществами? Сколько атомов должно быть в группировке, чтобы её уже нельзя было считать молекулой? Как и везде, абсолютно строгой границы нет, но на практике вопрос решается довольно просто. Обычные молекулы, с которыми работает большинство химиков, содержат до 100 атомов. Вещества, у которых в молекуле 10³ -10⁷ атомов, называются высокомолекулярными. С другой стороны, мельчайшая песчинка, с трудом видимая под микроскопом, диаметром в 1 мкм, содержит больше 10¹⁰ атомов, а лист оконного стекла - порядка 10²⁶ атомов. И все они связаны друг с другом, то есть образуют единую химическую структуру. Но молекулой её не называют, так как она не проявляет никаких свойств, присущих тому, что принято называть молекулами: не совершает теплового движения как единое целое (хотя внутри неё атомы, конечно, колеблются), неспособна переходить из одной фазы в другую (растворяться, испаряться) без потери химической индивидуальности. Атомы, находящиеся на поверхности песчинки, составляют 0,1 %, а на поверхности упомянутого листа - 10^-5 % общего числа атомов, и ими обычно пренебрегают при записи состава (хотя именно они в первую очередь вступают в химические реакции!).

Промежуточное по размеру положение между молекулами и частицами немолекулярного вещества занимают коллоидные частицы (или, по модной терминологии, наночастицы) - это либо очень большие молекулы, либо очень маленькие кусочки твёрдой фазы.

Представителем немолекулярного вещества является не молекула, а вся фаза (твёрдая или иногда жидкая). Реакции немолекулярных веществ - это обычно гетерогенные процессы, тогда как в химии молекулярных веществ основное значение имеют гомогенные реакции.

1.2.12. Смысл формул немолекулярных веществ. Формулы молекулярных веществ показывают истинное число атомов в молекуле. У немолекулярных веществ число химически связанных атомов неопределённо велико, и в учебниках химии по существующей традиции его даже не пытаются отразить, то есть заменяют истинную формулу на простейшую, которая отражает только состав, то есть соотношение компонентов, но не строение. Это вводит читателя в заблуждение. Ему приходится сравнивать вещества с похожими формулами, например, СО₂ и SiO₂, CaCO₃ и CaSiO₃, не видя главного различия между ними. Иногда и сами авторы учебников забывают об условном характере таких формул и всерьёз обсуждают строение и свойства несуществующих молекул и ионов, например, CaC₂, Al₂O₃, Sb₂O₅, AlO₂^-, SiO₃^2-, NbO₃^-, ZrO²⁺, Н₂B₄O₇ и т.п., игнорируя давно известные экспериментальные данные о структурах.

Если множество различных кристаллических и аморфных диоксидов кремния изображается одной формулой SiO₂ и считается одним веществом, то почему бы не изображать в виде СН₂ и не считать одним веществом все олефины (этен, пропен, бутен...) и все циклопарафины (циклопропан, циклобутан, циклопентан...), а также полиэтилен? Абсурдность этого предложения очевидна, но в неорганической химии подобный абсурд почему-то является нормой.

1.2.13. Нестехиометрия. Поскольку формула немолекулярного вещества показывает не число атомов, а лишь соотношение чисел атомов разных элементов, в ней возможны дробные и переменные индексы, то есть немолекулярные вещества могут, сохраняя свой тип структуры и не превращаясь в смесь веществ, иметь переменный состав. Три основных механизма нестехиометрии (три типа дефектов) - это вычитание (отсутствие некоторых атомов в тех местах структуры, которые обычно заняты), внедрение (присутствие добавочных атомов в тех местах структуры, которые обычно не заняты) и замещение одних атомов другими. Дефекты вычитания и внедрения - это не ошибки синтетика, а естественная принадлежность любой структуры, результат теплового движения. С точки зрения термодинамики их существование объясняется тем, что повышает энтропию.

Как согласовать нестехиометрию с правилами составления формул по валентностям или степеням окисления? Особенно легко отклонения от стехиометрии возникают там, где есть элементы с переменной степенью окисления, а также в структурах, где понятия валентности и степени окисления вовсе неприменимы, например, в металлических соединениях. Например, в так называемом оксиде железа (+2) со структурой NaCl всегда есть немного железа (+3), и содержание железа в кристаллах всегда меньше, чем кислорода: Fe_1-xO, где х всегда несколько больше нуля. Это не смесь оксидов, а единое вещество, где ионы, формально имеющие разную степень окисления, неразличимы, а электрон мигрирует между ними, обеспечивая электропроводность. В развёрнутом виде формулу можно записать как Fe²⁺_1-3xFe³⁺_2xO. Нестехиометричность широко распространена и среди соединений с постоянными степенями окисления, например, Na_1+xAl₁₁O_17+x/2.

1.2.14. Насколько распространены немолекулярные вещества? Поскольку ионные и металлические связи являются ненаправленными и ненасыщаемыми, практически все вещества с такими связями - немолекулярные. Что касается веществ, где основным типом связи является ковалентный, то они, в зависимости от валентностей и углов между связями, могут образовывать как молекулярные, так и немолекулярные структуры. С учётом сказанного становится ясно, что распространённое мнение, будто неорганических веществ меньше, чем органических, основано на неверном подсчёте формул. Разные по структуре вещества считаются одним веществом, нестехиометрические фазы обычно вообще не попадают в формульный указатель и не учитываются, а ведь каждая такая фаза - это серия из множества близких, но разных веществ (точно так же, как соседние члены гомологического ряда молекулярных веществ качественно близки, а отличаются лишь количественными характеристиками). При этом компонентов может быть не два, а больше, а их сочетаний - бесчисленное множество.

1.2.15. Деления веществ на молекулярные и немолекулярные недостаточно. Более содержательно деление по связности. Связность D (или пространственная размерность) структуры - это число измерений пространства, в которых непрерывна (практически бесконечна) система прочных связей. Очевидно, что D может принимать значения 0, 1, 2 и 3. Связность структуры - это самая важная её характеристика. При сопоставлении и прогнозе физико-химических свойств веществ нужно прежде всего обратить внимание на связность, а уже потом обсуждать природу и прочность отдельных связей. Авторы, не обращающие внимания на связность, считают само собой разумеющимся, что все вещества состоят из молекул, т.е. игнорируют случаи d = 1, 2, 3. Из учебников неорганической химии наибольшее (но всё же недостаточное) внимание связности уделено в книге Ахметова [13], наименьшее - в книгах Мартыненко и Спицына, Карапетьянца и Дракина.

Не следует путать связность (dimensionality, connectivity) с используемым в книге Уэллса понятием “связанность” (connectedness), которое означает число связей фрагмента структуры с другими фрагментами.

Совокупность атомов, соединённых прочными связями, обычно называют словом остов. Для атомов, ионов или молекул, не входящих в остов, не нашлось более благозвучного названия, чем начинка. Если в структуре есть несколько типов прочных связей, то в остов следует включать все достаточно прочные связи, обеспечивающие максимальное значение D. Дальнейшая классификация структур в зависимости от наличия заряда у остова и наличия начинки, дана в табл. 5.

Таблица 5. Классификация структур по связности

D	Остов не заряжен	Остов заряжен, есть начинка противоположного знака
начинки нет	есть нейтральная начинка
	молекулярные структуры	структуры с островными ионами
	цепочечные структуры
	слоистые структуры
	гомодесмичные структуры	каркасные структуры

1.2.16. Влияние связности на физические свойства известно ещё из школьного курса на примере аллотропных разновидностей углерода. Резкое различие между графитом и алмазом обусловлено не разным типом связи (он в обоих случаях ковалентный) и не прочностью связей (энергия атомизации у них почти одинакова, а отдельная связь СС в мягком графите короче и прочнее, чем связь СС в очень твёрдом алмазе), а различием в связности. В графите в одном из трёх измерений нет ковалентных связей, поэтому слои легко сдвигаются друг относительно друга (отсюда низкая механическая прочность и использование графита для смазки), что невозможно в алмазе без разрыва прочных ковалентных связей, поэтому он твёрд и хрупок. Всякий, кто видел слюду, поймёт, даже не зная её атомной структуры, что и для неё D=2. Но всё же эти вещества немолекулярные, поэтому имеют высокие температуры плавления, низкие летучесть и растворимость: чтобы оторвать отдельные атомы или группы атомов, нужно нарушать прочные ковалентные связи. Сильно отличаются от них ещё одна разновидность углерода - фуллерен С₆₀ (молекула в форме футбольного мяча) и ближайший сосед углерода по периодической системе - азот N₂. Здесь для плавления, испарения или растворения не нужно разрывать ковалентные связи, достаточно преодолеть межмолекулярное притяжение (особенно слабое в случае маленьких молекул азота) - отсюда легкоплавкость, летучесть, растворимость в подходящих растворителях.

Аналогично можно рассмотреть влияние связности и на другие свойства. Например, при образовании системы сопряжённых p-связей электроны свободно перемещаются между всеми атомами, входящими в эту систему, что придаёт графиту электропроводность в двух измерениях (D=2), тогда как в бензоле (D=0) p-электроны перемещаются лишь в пределах молекулы и не могут перескочить в соседнюю молекулу, поэтому бензол - диэлектрик.

При близких характере и прочности связи немолекулярные вещества обычно менее химически активны, чем молекулярные, и вступают в реакции тем труднее, чем выше D. Поэтому до сих пор в умах некоторых химиков сохранилось старинное правило “вещества не реагируют, если они не жидкие”. Это всё же неверно. Существуют и чисто твердофазные реакции, происходящие путём диффузии одного или нескольких компонентов через слой твёрдого продукта (если продукт жидкий или газообразный, он обычно не создаёт диффузионных затруднений). Возможность такой диффузии сильно зависит от дефектности и типа структуры продукта. Обычно для твердофазной диффузии требуются высокие температуры. Типичные примеры - синтез силикатов и алюминатов кальция на цементных заводах, синтез ферритов, титанатов, цирконатов при производстве электротехнической керамики. Высокотемпературное окисление стали также происходит путём диффузии железа через слой оксида, и подавить такую диффузию - значит повысить жаростойкость стали.

Но известно и множество реакций немолекулярных веществ с сохранением остова- “мягкая химия твёрдого тела” -ионный обмен, внедрение, вычитание, замещение ионов в готовом жёстком остове, которые опять-таки зависят от связности. Например, внедрение атомов или молекул легко происходит в графите и практически невозможно в алмазе. В подобных реакциях весь кристалл участвует как одно целое. Он превращается в другое вещество, сохраняя свою форму и все свои царапины.

1.3. Систематика координационных групп (см. табл. 6 и рис. 1)

1.3.1. Названия координационных групп АХ_n - это обычно названия многогранников (полинговских полиэдров), которые получаются, если соединить отрезками прямых атомы Х между собой и с атомом А. Но для химии обычно важны связи А-Х с центральным атомом, а не ребра Х-Х, и не грани. Слово “октаэдр” значит восьмигранник, но он нас обычно интересует, как шестивершинник. “Шапка” в названии фигуры означает дополнительную вершину, расположенную против центра одной из граней. Естественно, размеры грани с шапкой уже не такие, как без шапки. Термины “пирамида”, “призма” и названия пяти правильных многогранников (тел Платона) должны быть известны из школьной геометрии, бипирамида (или дипирамида) означает две пирамиды, соединённые общим основанием, n-угольная антипризма - это результат поворота одного основания n-угольной призмы в своей плоскости на угол 180°/n. Боковые грани у неё - не прямоугольники, а треугольники. Дельтадодекаэдр отличается от правильного (платоновского) додекаэдра: грани его треугольные (дельтавидные), и вершин не 20, а 8.

1.3.2. Способы изображения координационных групп:

- масштабные модели из вдавленных друг в друга шаров разного размера; они правильно передают соотношение атомных размеров и перекрывание электронных оболочек, но тяжелы, непрозрачны и потому дают плохое представление о валентных углах и межъядерных расстояниях;

- шаростержневые модели, введённые Дальтоном, где шарики изображают не атомы, а их центры; они наиболее употребительны, только не надо забывать, что в реальных структурах атомы соединены не стержнями, а электростатическими силами, и “пустые” промежутки заняты электронными оболочками;

- многогранники, где центральный атом А вовсе не виден, а окружающие его атомы Х изображены точками - вершинами; такое изображение, впервые использованное Вант-Гоффом и впоследствии широко внедрённое Полингом, кажется слишком отвлечённым, но оно удобно при рассмотрении сложных структур из большого числа координационных групп;

Таблица 6. Некоторые наиболее симметричные координации АX_n

(Последняя колонка оставлена для самостоятельного заполнения

студентами)

n (КЧ)	Название, расположение по уровням вдоль главной оси симметрии	Углы ХАХ,°	RA/RX	Cимметрия	Примечания Примеры
	Гантель (линейное) 1-1		³ 0	D¥h
	Плоский треугольник 3	3 по 120	³ 0,15	D3h
	Тетраэдр 2-2 (1-3)	6 по 109,5	³ 0,22	Td
	Плоский квадрат 4	4 по 90	³ 0,41	D4h
	Треугольная бипирамида 1-3-1	6 по 90, 3 по 120	³ 0,41	D3h
	Квадратная пирамида 1-4	8 по 90	³ 0,41	C4v
	Октаэдр 1-4-1 (3-3)	12 по 90	³ 0,41	Oh
	Треугольная призма 3-3	9 по 81,8	³ 0,53	D3h
	Одношапочный октаэдр 1-3-3	12 по 77,9, 3 по 115,7	³ 0,59	C3v
	Одношапочная треугольная призма 1-4-2	11 по 77,3, 2 по 97,1	³ 0,60	C2v
	Пятиугольная бипирамида 1-5-1	5 по 72, 10 по 90	³ 0,70	D5h
	Квадратная антипризма 4-4	16 по 74,8	³ 0,645	D4d
	Бисбисфеноид 2-2-2-2 (дельтадодекаэдр)	14 по 73,7 4 по 97,1	³ 0,67	D2d
	Куб 4-4 (1-3-3-1)	12 по 70,5	³ 0,73	Oh
	Шестиугольная бипирамида 1-6-1	6 по 60 12 по 90	³ 1	D6h
	Трехшапочная треугольная призма 3-3-3	18 по 70,5 3 по 96,4	³ 0,73	D3h
	Одношапочная квадратная антипризма 1-4-4	16 по 70,1 4 по 83,3	³ 0,74	C4v
	Двухшапочная квадратная антипризма 1-4-4-1	16 по 65,5, 8 по 80,1	³ 0,85	D4d
	Пятиугольная антипризма 5-5	20 по 63,4	³ 0,90	D5d
	Одношапочная пятиугольная антипризма 1-5-5	25 по 63,4	³ 0,90	C5v
	Пятишапочная треугольная призма 1-3-3-3-1	9 по 60, 12 по 64,3, 6 по 97,2	³ 1	D3h
	Икосаэдр 1-5-5-1 (3-3-3-3)	30 по 63,4	³ 0,90	Ih
	Кубооктаэдр 4-4-4 (3-6-3)	24 по 60	³ 1	Oh
	Скрученный кубооктаэдр 3-6-3	24 по 60	³ 1	D3h

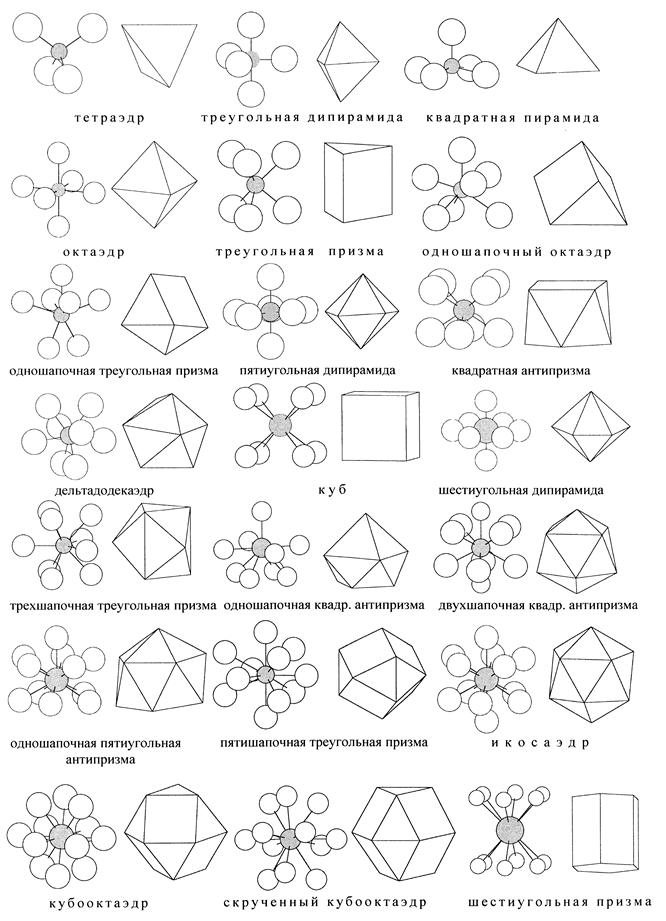
Рис. 1. Шаростержневые и полиэдрические изображения наиболее симметричных

координационных групп c КЧ 4-12, перечисленных в табл. 6

- структурные формулы на бумаге, где символы элементов соединены чёрточками; чёрточки, выходящие из плоскости бумаги, изображаются в перспективе - с утолщённым ближним концом; именно этот способ рекомендуется студентам.

Наряду с объёмными моделями в последнее время всё чаще используются компьютерные изображения, которые можно вращать и редактировать. Описания множества структур доступны через электронные базы данных и электронные приложения к кристаллографическим журналам.

В табл. 6 форма также описана последовательностью цифр. Чтобы восстановить по ней форму, нужно провести вокруг центрального атома сферу, провести через него диаметр - ось симметрии фигуры, провести перпендикулярные диаметру плоскости (по числу цифр), и на пересечениях со сферой (окружностях) разместить подальше друг от друга указанное число точек - вершин многогранника.

При данном КЧ разные формы окружения можно также различать по их симметрии. Но если КЧ не указано, то одной симметрии недостаточно. Например, октаэдр, куб и их сочетание - кубооктаэдр - имеют одинаковую симметрию. Оси симметрии пятого, седьмого и более высоких порядков несовместимы с кристаллической решёткой, поэтому фигуры с такими осями будут в кристаллах неизбежно искажены, хотя, может быть, и не сильно.

1.3.3. Валентные углы ХАХ для некоторых координаций однозначно следуют из симметрии. Например, в правильном тетраэдре АХ₄ все углы - по 109,5°. Реально некоторые углы могут быть меньше, а некоторые больше, но это уже будет искажённый тетраэдр. Но для многих координаций валентные углы не вытекают из симметрии. Например, в правильной треугольной призме АХ₆ есть шесть равных углов ХАХ, соответствующих ребрам оснований, и три других угла, соответствующих боковым ребрам. Если призму растягивать или сжимать вдоль оси третьего порядка, то можно, сохраняя симметрию, увеличивать меньшие углы, одновременно уменьшая большие. В какой-то момент эти углы становятся равными. В табл. 6 приведены именно такие максиминные значения - максимально возможные значения минимального угла для каждой координации. Реально некоторые углы могут быть и больше, но при этом неизбежно другие будут меньше указанных значений. Группы с одинаковым КЧ в табл. 6 расположены в порядке уменьшения максиминного угла, а при одинаковом максиминном угле - в порядке возрастания числа малых углов. Поэтому группа, указанная первой при каждом КЧ, обеспечивает наибольшее удаление вершин друг от друга.

1.4. Ограничения координации, не зависящие от характера химической связи

При ионном и металлическом (а иногда и при ковалентном) характере связи КЧ могут быть намного больше формальной валентности, но это не значит, что они могут быть любыми. Есть ряд строгих ограничений, которые и рассматриваются в данном разделе.

1.4.1. Условие координационного баланса. Это условие - наиболее общее и очевидное, тем не менее в учебниках неорганической химии оно не приводится, а ошибки, связанные с его незнанием, встречаются очень часто.

В любой структуре общее количество контактов атомов А с атомами Х равно общему количеству контактов атомов Х с атомами А, так как это одни и те же контакты.

Рассмотрим соединение с простейшей формулой А_mB_n...X_pY_q..., где A, B, X, Y - разные элементы или атомы одного элемента с разным окружением. Для любой пары видов атомов справедливы соотношения:

m(КЧ А по Х) = p(КЧ Х по А); n(КЧ В по Х) = р(КЧ Х по В) и т.д.

Таким образом, если известна простейшая формула соединения и КЧ некоторых атомов, то можно вычислить КЧ других атомов. Но если атомы одного элемента имеют разные КЧ, а мы этого не учитываем, то по формуле будет получаться их усреднённое КЧ. Конечно, атом А может быть одновременно связан с атомами разных видов (в том числе и с одноимёнными), но в каждом уравнении учитываются контакты только одной пары видов.

Понятие КЧ не вполне строгое (п. 1.2.2). Не значит ли это, что и уравнение координационного баланса нестрогое? - Нет, не значит. Если какой-то контакт А-Х мы учли при анализе окружения А, то он должен быть учтён и при анализе окружения Х. А связь ли это на самом деле - для данного уравнения неважно.

Пример. Найти КЧ кислорода по ниобию и хрому в соединениях Na₃Cr(OH)₆, Cr(OH)₃, KNbO₃ и Nb₂O₅, зная, что для хрома (3+) и ниобия (5+) весьма характерна октаэдрическая координация.

Решение. (КЧ О по М) = 6m/p = 1, 2, 2 и 2,4 соответственно. Таким образом, в первом соединении все гидроксилы - концевые, и гидроксокомплекс островной, а во всех остальных соединениях гидроксилы или атомы кислорода - мостиковые, и структуры полимерные.

Но как понимать дробное КЧ кислорода в оксиде ниобия? Иногда говорят: “там есть более прочные и менее прочные связи, которые нельзя считать за целую связь”. Даже если связи и неравноценны, это рассуждение не объясняет дробного КЧ. Ведь когда указывалось КЧ металла, все связи считались как целые, почему же при обсуждении КЧ неметалла они учитываются иначе? Если это не связь - не учитывайте ее ни у металла, ни

Дата добавления: 2015-07-25