
Читайте также:
|
Относится к частотным и основан на исследовании характерной функции D(jω)=U(ω)+jV(ω) полученной из характерного уравнения системы подстановкой p=jω.
Составим годограф функции:
D(p) = 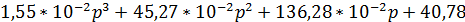 .
.
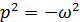 .
.
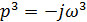 .
.
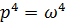 .
.
D(jω) = 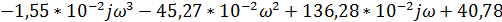 .
.
Делим на действительную и мнимую части и находим значения при которых уравнения будут равны нулю:
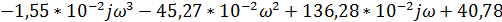 = 0.
= 0.
Действительная часть:
U(ω) = 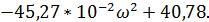
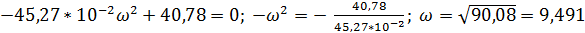 .
.
Мнимая часть:
jV(ω) = 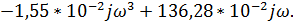
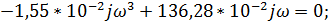
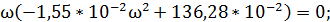
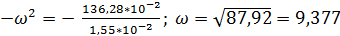 .
.
Составляем таблицу 3 по результатам расчетов:
U(0) = 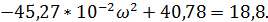
U(9,377) = 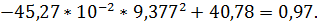
U(9,491) = 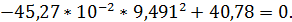
jV(0) = 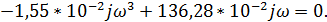
jV(9,377) = 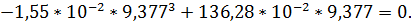
jV(9,491) = 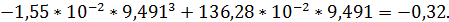
Таблица 3
| ω | U(ω) | V(ω) |
| 40,78 | 0,00 | |
| 9,377 | 0,97 | 0,00 |
| 9,491 | 0,00 | -0,32 |
| ∞ | -∞ | -∞ |
По данным таблицы 3 строим годограф Михайлова (рис. 6).

Рисунок 6 – годограф Михайлова
Система неустойчива, так как годограф проходит по часовой стрелки.
Дата добавления: 2015-07-25; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оценка устойчивости системы по критерию Найквиста | | | Исследование системы стабилизации частоты вращения двигателя с введением корректирующего звена |