Це розділ математики, в якому геометричні об’єкти вивчають засобами алгебри на основі метода координат. Виникла в 17 ст. Декарт.
Предметом аналітичної геометрії є вивчення геометричніх образів алгебраічними методами.
Засоби досліджень: метод координат і алгебра.
Кожна точка на площині ототожнюється з упорядкованою парою, а в просторі – з трійкою чисел – координатами цієї точки.
Найпростіші задачі аналітичної геометрії:
1. Відстань між 2 точками. 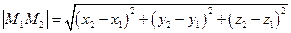 для М1 для М1 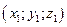 і М2 і М2 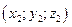 2. Ділення відрізка в заданому відношенні.
М1
2. Ділення відрізка в заданому відношенні.
М1 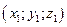 і М2 і М2 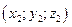 . Точка М(х; у; z) поділяє відрізок М1 М2 в данному відношені: . Точка М(х; у; z) поділяє відрізок М1 М2 в данному відношені: 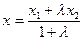 , , 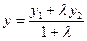 , , 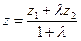 .
Якщо точка М поділяє відрізок навпіл: .
Якщо точка М поділяє відрізок навпіл: 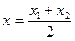 , , 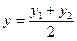 , , 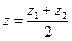 Основні задачі аналітичної геометрії:
1. Складання рівняння геометричного об’єкта, який розглядають як ГМТ – геометричне місце точок.
2. Дослідження і побудова геометричного об’єкта за його рівнянням.
Основні поняття:
Найпростіші геометричні образи:точки, прямі, площини, криві, поверхні 2 порядку.
Вісь –пряма лінія з вказани на ній напрямком.
Напрямлений –відрізок на вісі, якщо вказано яка з його граничних точок є початком і є кінцем.
Нульовий відрізок –напрямлений відрізок, коли точки початку і кінця співпадають.
Величина напрямленого відрізку –число, що дорівнює довжині відрізка (із знаком „+”, коли напрямок відрізка співпадає з напрямком вісі та із знаком „-„ в протилежному.
2 ненульові напрямлені відрізка рівні, якщо при суміщенні їх початків співпадають їх кінці.
Основні задачі аналітичної геометрії:
1. Складання рівняння геометричного об’єкта, який розглядають як ГМТ – геометричне місце точок.
2. Дослідження і побудова геометричного об’єкта за його рівнянням.
Основні поняття:
Найпростіші геометричні образи:точки, прямі, площини, криві, поверхні 2 порядку.
Вісь –пряма лінія з вказани на ній напрямком.
Напрямлений –відрізок на вісі, якщо вказано яка з його граничних точок є початком і є кінцем.
Нульовий відрізок –напрямлений відрізок, коли точки початку і кінця співпадають.
Величина напрямленого відрізку –число, що дорівнює довжині відрізка (із знаком „+”, коли напрямок відрізка співпадає з напрямком вісі та із знаком „-„ в протилежному.
2 ненульові напрямлені відрізка рівні, якщо при суміщенні їх початків співпадають їх кінці.
|

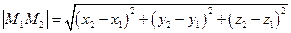 для М1
для М1 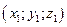 і М2
і М2 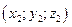 2. Ділення відрізка в заданому відношенні.
М1
2. Ділення відрізка в заданому відношенні.
М1 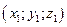 і М2
і М2 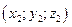 . Точка М(х; у; z) поділяє відрізок М1 М2 в данному відношені:
. Точка М(х; у; z) поділяє відрізок М1 М2 в данному відношені: 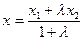 ,
, 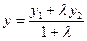 ,
, 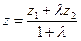 .
Якщо точка М поділяє відрізок навпіл:
.
Якщо точка М поділяє відрізок навпіл: 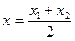 ,
, 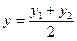 ,
, 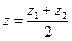 Основні задачі аналітичної геометрії:
1. Складання рівняння геометричного об’єкта, який розглядають як ГМТ – геометричне місце точок.
2. Дослідження і побудова геометричного об’єкта за його рівнянням.
Основні поняття:
Найпростіші геометричні образи:точки, прямі, площини, криві, поверхні 2 порядку.
Вісь –пряма лінія з вказани на ній напрямком.
Напрямлений –відрізок на вісі, якщо вказано яка з його граничних точок є початком і є кінцем.
Нульовий відрізок –напрямлений відрізок, коли точки початку і кінця співпадають.
Величина напрямленого відрізку –число, що дорівнює довжині відрізка (із знаком „+”, коли напрямок відрізка співпадає з напрямком вісі та із знаком „-„ в протилежному.
2 ненульові напрямлені відрізка рівні, якщо при суміщенні їх початків співпадають їх кінці.
Основні задачі аналітичної геометрії:
1. Складання рівняння геометричного об’єкта, який розглядають як ГМТ – геометричне місце точок.
2. Дослідження і побудова геометричного об’єкта за його рівнянням.
Основні поняття:
Найпростіші геометричні образи:точки, прямі, площини, криві, поверхні 2 порядку.
Вісь –пряма лінія з вказани на ній напрямком.
Напрямлений –відрізок на вісі, якщо вказано яка з його граничних точок є початком і є кінцем.
Нульовий відрізок –напрямлений відрізок, коли точки початку і кінця співпадають.
Величина напрямленого відрізку –число, що дорівнює довжині відрізка (із знаком „+”, коли напрямок відрізка співпадає з напрямком вісі та із знаком „-„ в протилежному.
2 ненульові напрямлені відрізка рівні, якщо при суміщенні їх початків співпадають їх кінці.