
Читайте также:
|
Це впорядковані таблиці числових або літерних значень з m рядків та n стовпців
А  , , 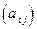 або А = або А = 
|
Характеристики матриць:
1. Елементи 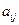 - величини, що входять до матриці (і – номер рядка, j – стовпця) і знаходятьсмя на перетині і –го рядка, j – стовпця. - величини, що входять до матриці (і – номер рядка, j – стовпця) і знаходятьсмя на перетині і –го рядка, j – стовпця.  , ,  2. Розмір матриці
2. Розмір матриці  -зумовлений кількістю його рядків і стовпців.
3. Головна діагональ –спрямована зверху донизу, зліва направо.
4. Побічна діагональ – протилежна головній діагоналі.
5. Алгебраічні доповнення -зумовлений кількістю його рядків і стовпців.
3. Головна діагональ –спрямована зверху донизу, зліва направо.
4. Побічна діагональ – протилежна головній діагоналі.
5. Алгебраічні доповнення 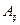 (ад’юнкта) елементів (ад’юнкта) елементів 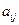 -мінори цих елементів, взяті із знаком -мінори цих елементів, взяті із знаком  : : 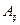 = =   6.
6.  - мінор елемента - мінор елемента 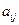 - визначник на порядок нищий попереднього визначника, що залишається після викреслювання рядка та стовпця, які стоять на їх перетині.
7. Пропорційні рядки (стовпці) –якщо елементи одного з них отримані з іншого домноженням на одне число.
8. Транспонування – математична операція, при якій рядки становляться відповідними стовпцями.
9.Елементи з однаковими індексами - визначник на порядок нищий попереднього визначника, що залишається після викреслювання рядка та стовпця, які стоять на їх перетині.
7. Пропорційні рядки (стовпці) –якщо елементи одного з них отримані з іншого домноженням на одне число.
8. Транспонування – математична операція, при якій рядки становляться відповідними стовпцями.
9.Елементи з однаковими індексами  називаються діагональними.
10.Матриці еквівалентні,якщо одна з них отримана з іншої
шляхом елементарних перетворень. А ~ В. називаються діагональними.
10.Матриці еквівалентні,якщо одна з них отримана з іншої
шляхом елементарних перетворень. А ~ В.
|
Види матриць:
| № | Назва та означення | Формула |
| Матриця - рядок |  , , 
| |
| Матриця - стовпець |  , , 
| |
Квадратнаматриця –
якщо кількість рядків і стовпців однакові: 
| 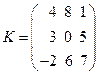 , , 
| |
Прямокутнаматриця –
якщо кількість рядків і стовпців різні: 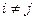
|  , , 
| |
| Нульова матриця – якщо всі елементи дорівнюють нулю. |  , , 
| |
| Особлива (вироджена) -квадратнаматриця, виз-начник якої дорівнює 0. |  , , 
| |
| Невироджена -квадратнаматриця, визначник якої відмінний від нуля. |  , , 
| |
| Ступінчата -квадратнаматриця, якщо в окремих рядках один елемент відмінний від 0, а всі інші дорівнюють нулю. |
 , , 
| |
| Діагональна -ступінчатаматриця, якщо відмінні від 0 елементи стоять на головній діагоналі. |
 , , 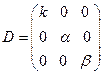
| |
| Скалярна -діагональнаматриця, елементи якої рівні між собою. |  , , 
| |
| Одинична –скалярна матриця, елементи якої на головній діагоналі 1. |  . .
|
Дії над матрицями
| Матрицю неможливо обчислити! |
| При будь-яких діях над матрицями завжди отримують матрицю. |
Матриці рівнітоді і тільки тоді, коли вони мають однаковий розмір та однакові відповідні елементи:
А = В 
|
| № | Дія, закон | Формула |
| Додавання матриць. Сума двох матриць А і В – інша матриця, кожен елемент якої дорівнює сумі відповідних елементів матриць А і В. |
 + +  = =  А + В = С,тобто
А + В = С,тобто 
| |
| Віднімання матриць. Різниця двох матриць А і В – інша матриця, кожен елемент якої дорівнює різниці відповідних елементів матриць А і В. |
 - -  = =  А - В = Д,тобто
А - В = Д,тобто 
| |
| Множення матриць на число. Добутком матриці А на число k – інша матриця, кожен елемент якої дорівнює добутку відповідних елементів матриці А на число k. |
kА = k  = =  kА = С,тобто
kА = С,тобто 
| |
| Множення матриць. Добуток двох матриць А і В – інша матриця, кожен елемент якої дорівнює сумі добутків елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці В. |
А∙В=  ∙ ∙  = = = =  ,
А∙В = С,де ,
А∙В = С,де 

| |
| Піднесення матриці А до степеня n (можливе лише для квадратних матриць) – множення матриці саму на себе n разів. |
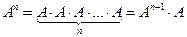
| |
| Транспонуванняматриць | А =  , , 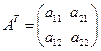
| |
| Обертання– процес знаходження оберненої матриці | А-1 = 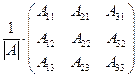
| |
| Діленняматриць |  = С, де В-1 – обернена до В матриця = С, де В-1 – обернена до В матриця
|
Властивості матриць:
| Добуток прямокутних матриць існує лише тоді, коли кількість стовпців лівої матриці дорівнює кількості рядків правої матриці. |
| Лише квадратну матрицю можна множити саму на себе. |
| 1) А + В = В + А А, В, С, Е - матриці 2) А + 0 = А α, β - числа 3) АЕ = ЕА = А 4) А + (В + С) = (А + В) + С = А + В + С 5) k(А + В) = kА + kВ 6) (α + β)∙А = αА + βА 7) α(β∙А) = (αβ)А 8) А(ВС) = (АВ)С = АВС 9) α(АВ) = А(αВ) = (αА)В = αАВ 10) (А + В)С = АС + ВС 11) С(А + В) = СА + ВС 12) 1∙ А = А 13) А∙ А-1 = Е, де А-1 – обернена. |
Специфічні властивості матриць:
1) А∙ В  В ∙ А
2) Якщо А∙ В та В ∙ А існують, то отримані матриці можуть бути різних розмірів.
3) А∙ В існує, а В ∙ А можливо не існує.
4) А∙ В = 0, то з цього не випливає, що В =0, або А = 0. В ∙ А
2) Якщо А∙ В та В ∙ А існують, то отримані матриці можуть бути різних розмірів.
3) А∙ В існує, а В ∙ А можливо не існує.
4) А∙ В = 0, то з цього не випливає, що В =0, або А = 0.
|
Властивості транспонованих матриць:
1) 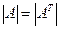 :Визначники квадратної і транспонованої матриць рівні.
2) Атт = (Ат)т = А, тобто 2 рази транспонована матриця дорівнює
попередній матриці.
3) А :Визначники квадратної і транспонованої матриць рівні.
2) Атт = (Ат)т = А, тобто 2 рази транспонована матриця дорівнює
попередній матриці.
3) А  , Ат , Ат  .4)(kА)т = kАт
5) (А + В)т = Ат + Вт 6) (АВ)т = ВтАт .4)(kА)т = kАт
5) (А + В)т = Ат + Вт 6) (АВ)т = ВтАт
|
Алгоритми знаходження оберненої матриці:
Дата добавления: 2015-07-25; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обчислення визначників | | | Ранг матриці |