Лінійна залежність рядків(стовпців) матриці означає, що хоча би один рядок (стовпець) є лінійною комбінацією інших.
Необхідна і достатня умова лінійної залежності рядків (стовпців) матриці є те, що один з них є лінійною комбінацією інших.
Теорема про ранг: Рядки та стовпці матриці, елементи яких входять в базисний мінор, лінійно незалежні. Будь-який рядок або стовпець матриці є лінійною комбінацією цих рядків (стовпців).
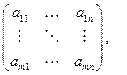  , , 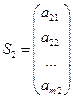 ... ...  ,..., ,..., 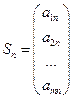 Стовпець
Стовпець  -лінійна комбінація стовпців -лінійна комбінація стовпців  , ,  ,..., ,...,  , якщо його можна представити у вигляді: , якщо його можна представити у вигляді:  = =  + +  +... + +... +  , де , де
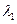 , , 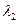 ,..., ,..., 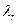 - деякі числа.
Стовпці - деякі числа.
Стовпці  , ,  ,..., ,...,  називаються лінійно залежними,якщо існують числа називаються лінійно залежними,якщо існують числа 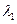 , , 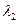 ,..., ,..., 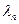 , які одночасно не рівні нулю, що їх лінійна комбінація стовпців дорівнюють нульовому стовпцю: , які одночасно не рівні нулю, що їх лінійна комбінація стовпців дорівнюють нульовому стовпцю:
 = =  + +  +... + +... +  = 0.
Якщо лінійна комбінація стовпців дорівнюють нульовому стовпцю тоді і тільки тоді, коли усі коефіцієнти = 0.
Якщо лінійна комбінація стовпців дорівнюють нульовому стовпцю тоді і тільки тоді, коли усі коефіцієнти 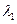 , , 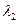 ,..., ,..., 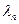 дорівнюють нулю, то стовпці дорівнюють нулю, то стовпці  , ,  ,..., ,...,  лінійно незалежні. лінійно незалежні.
|

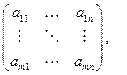
 ,
, 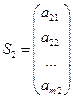 ...
...  ,...,
,...,  Стовпець
Стовпець  -лінійна комбінація стовпців
-лінійна комбінація стовпців  ,
,  ,...,
,...,  , якщо його можна представити у вигляді:
, якщо його можна представити у вигляді:  =
=  +
+  +... +
+... +  , де
, де
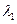 ,
, 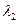 ,...,
,..., 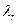 - деякі числа.
Стовпці
- деякі числа.
Стовпці  ,
,  ,...,
,...,  називаються лінійно залежними,якщо існують числа
називаються лінійно залежними,якщо існують числа 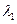 ,
, 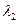 ,...,
,..., 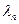 , які одночасно не рівні нулю, що їх лінійна комбінація стовпців дорівнюють нульовому стовпцю:
, які одночасно не рівні нулю, що їх лінійна комбінація стовпців дорівнюють нульовому стовпцю:
 =
=  +
+  +... +
+... +  = 0.
Якщо лінійна комбінація стовпців дорівнюють нульовому стовпцю тоді і тільки тоді, коли усі коефіцієнти
= 0.
Якщо лінійна комбінація стовпців дорівнюють нульовому стовпцю тоді і тільки тоді, коли усі коефіцієнти 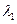 ,
, 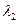 ,...,
,..., 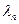 дорівнюють нулю, то стовпці
дорівнюють нулю, то стовпці  ,
,  ,...,
,...,  лінійно незалежні.
лінійно незалежні.