
Читайте также:
|
Це сукупність скінченої кількості лінійних рівнянь, розв’язком
якої є точка, яка є розв’язком кожного її рівняння.
Система m лінійних рівнянь з n невідомими:
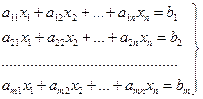 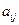 - коефіцієнти, - коефіцієнти, 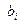 -вільні члени (числа).
Можливо: m – число рівнянь, n – число невідомих.
1) m > n -вільні члени (числа).
Можливо: m – число рівнянь, n – число невідомих.
1) m > n 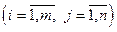 2)m = n 1 рішення
3) m < n безліч рішень
Розв’язок системи рівнянь –це набір чисел (
2)m = n 1 рішення
3) m < n безліч рішень
Розв’язок системи рівнянь –це набір чисел (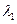 , , 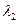 ,..., ,..., 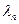 ),
який є рішенням кожного рівняння системи, тобто це сукупність невідомих ( ),
який є рішенням кожного рівняння системи, тобто це сукупність невідомих (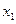 , , 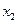 ,..., ,..., 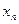 ), яка при підстановці в рівняння системи перетворює кожне рівняння системи у тотожність. ), яка при підстановці в рівняння системи перетворює кожне рівняння системи у тотожність.
|
Види систем:
Система однорідна,якщо всі вільні члени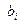 = 0. Вона завжди сумісна. = 0. Вона завжди сумісна.
|
Якщо хоча би один з вільних членів 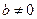 , то система неоднорідна. , то система неоднорідна.
|
| Система сумісна,якщо вона має хоча би 1 рішення. |
| Система несумісна,якщо вона не має жодного рішення. |
| Сумісна система визначена,якщо вона має 1 рішення. |
| Сумісна система невизначена,якщо вона має декілька рішень. |
| 2 системи рівнянь еквівалентні,якщо вони мають одну і ту ж множину рішень. |
| 2 системи рівнянь рівносильні,якщо вони мають однакові рішення |
Дата добавления: 2015-07-25; просмотров: 45 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЛІНІЙНІ РІВНЯННЯ | | | Критерій сумісності системи рівнянь |