Теорема Кронекера – Капелі.Для сумісної системи лінійних рівнянь необхідно і достатньо, щоб ранг матриці системи дорівнював би рангу розширеної матриці:   . .
 - матриця системи (з коефіцієнтів при невідомих). - матриця системи (з коефіцієнтів при невідомих).
 - розширена матриця.
Наслідки:
1.Будь-який мінор А є мінором А*, тому ранг матриці системи не перевищує рангу розширеної матриці: - розширена матриця.
Наслідки:
1.Будь-який мінор А є мінором А*, тому ранг матриці системи не перевищує рангу розширеної матриці:  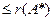 .
2.Якщо при виконанні умови сумісності системи .
2.Якщо при виконанні умови сумісності системи  , то система має 1 розв’язок.
3.Якщо при виконанні умови сумісності системи , то система має 1 розв’язок.
3.Якщо при виконанні умови сумісності системи  , то система має безліч р розв’язків, тобто стовпець вільних членів є лінійною комбінацією базисних стовпців , то система має безліч р розв’язків, тобто стовпець вільних членів є лінійною комбінацією базисних стовпців  , ,  ,..., ,...,  . .
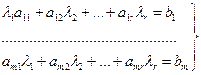   = =  + +  +... + +... +  4.Якщо ранг матриці системи співпадає з рангом розширеної матриці, то система розв’язків не має.
5.У системі стільки лінійно-незалежних розв’язків (всі інші – їх комбінації), яка різниця між числом невідомих і рангом матриці системи.
4.Якщо ранг матриці системи співпадає з рангом розширеної матриці, то система розв’язків не має.
5.У системі стільки лінійно-незалежних розв’язків (всі інші – їх комбінації), яка різниця між числом невідомих і рангом матриці системи.
|


 .
.
 - матриця системи (з коефіцієнтів при невідомих).
- матриця системи (з коефіцієнтів при невідомих).
 - розширена матриця.
Наслідки:
1.Будь-який мінор А є мінором А*, тому ранг матриці системи не перевищує рангу розширеної матриці:
- розширена матриця.
Наслідки:
1.Будь-який мінор А є мінором А*, тому ранг матриці системи не перевищує рангу розширеної матриці: 
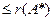 .
2.Якщо при виконанні умови сумісності системи
.
2.Якщо при виконанні умови сумісності системи  , то система має 1 розв’язок.
3.Якщо при виконанні умови сумісності системи
, то система має 1 розв’язок.
3.Якщо при виконанні умови сумісності системи  , то система має безліч р розв’язків, тобто стовпець вільних членів є лінійною комбінацією базисних стовпців
, то система має безліч р розв’язків, тобто стовпець вільних членів є лінійною комбінацією базисних стовпців  ,
,  ,...,
,...,  .
.
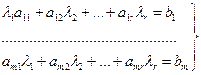

 =
=  +
+  +... +
+... +  4.Якщо ранг матриці системи співпадає з рангом розширеної матриці, то система розв’язків не має.
5.У системі стільки лінійно-незалежних розв’язків (всі інші – їх комбінації), яка різниця між числом невідомих і рангом матриці системи.
4.Якщо ранг матриці системи співпадає з рангом розширеної матриці, то система розв’язків не має.
5.У системі стільки лінійно-незалежних розв’язків (всі інші – їх комбінації), яка різниця між числом невідомих і рангом матриці системи.