
Розрізняють скалярні величини та векторні.
Скалярна –величина, яка характеризується числовим значенням (модулем).
Вектор -величина, яка характеризується не лише числовим значенням, а й напрямком. 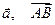 Нульовий –вектор, у якого початок і кінець співпадають, довжина дорівнює нулю. Він не має напрямку – напрям довільний.
Нульовий –вектор, у якого початок і кінець співпадають, довжина дорівнює нулю. Він не має напрямку – напрям довільний.
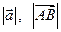 - довжина вектора (модуль) – це відстань між його початком та кінцем: - довжина вектора (модуль) – це відстань між його початком та кінцем: 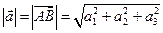 .
Колінеарні - вектори, які лежать на одній прямій або на паралельних прямих. Кут між ними дорівнює 0, відповідні координати пропорційні .
Колінеарні - вектори, які лежать на одній прямій або на паралельних прямих. Кут між ними дорівнює 0, відповідні координати пропорційні 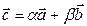 .
Вектори рівні,якщо вони сполучаються паралельним переносом (рівні за величиною та співпадають за напрямком). У них рівні координати, довжини та напрями. Це колінеарні вектори.
Одиничний –вектор, довжина якого дорівнює одиниці.
Протилежні –паралельнівектори з однаковою довжиною і протилежного напрямку.
Компланарні - вектори, які лежать в одній площині або на паралельних площинах.
Вільні –вектори, початкова точка яких оберається довільно.
Приєднані (зв’язані) –вектори, для яких важлива точка приложення. .
Вектори рівні,якщо вони сполучаються паралельним переносом (рівні за величиною та співпадають за напрямком). У них рівні координати, довжини та напрями. Це колінеарні вектори.
Одиничний –вектор, довжина якого дорівнює одиниці.
Протилежні –паралельнівектори з однаковою довжиною і протилежного напрямку.
Компланарні - вектори, які лежать в одній площині або на паралельних площинах.
Вільні –вектори, початкова точка яких оберається довільно.
Приєднані (зв’язані) –вектори, для яких важлива точка приложення.
|
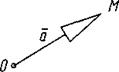
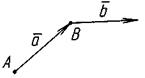
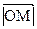 О – початок, М – кінець
О – початок, М – кінець
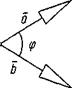
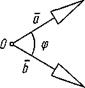 Кут між векторами - кут між рівними їм векторами з загальним початком.
Координати
Кут між векторами - кут між рівними їм векторами з загальним початком.
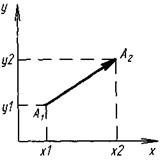
Координати 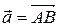 , де А(х1,у1), В(х2;у2) - числа а1 = х2 – х1, а1 = у2 – у1, тобто , де А(х1,у1), В(х2;у2) - числа а1 = х2 – х1, а1 = у2 – у1, тобто 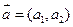 Властивості суми:
1.
Властивості суми:
1. 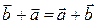 2.
2. 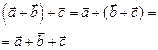 3.
3. 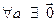 , що , що 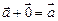 4.
4. 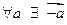 , що , що 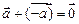
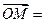 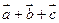
| Колінеарні вектори: 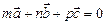 або або 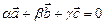 . m, n, р – числа . m, n, р – числа
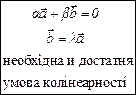 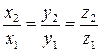 Операции над векторами.
На площині:
Додавання:
Операции над векторами.
На площині:
Додавання: 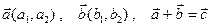
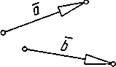 1. Правило треугольников.
1. Правило треугольников.
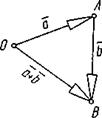 2. Правило параллелограмма.
2. Правило параллелограмма.
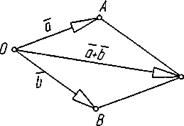 3. Правило многокутника.
3. Правило многокутника.
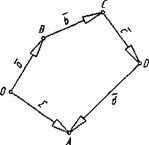 У просторі:
У просторі:
| |||||||||
Різниця 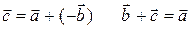

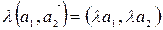 Вектор
Вектор 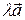 :
а) збільшений у λ раз, якщо λ>1
б) в λ раз зменшений, якщо
0< λ< 1
в) протилежно спрямований, якщо
λ < 0. :
а) збільшений у λ раз, якщо λ>1
б) в λ раз зменшений, якщо
0< λ< 1
в) протилежно спрямований, якщо
λ < 0.
| Різниця– це третій вектор, проведений із кінця віднімаємого до кінця зменшуваного, який при складанні з вектором 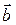 дає вектор дає вектор 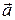 . .
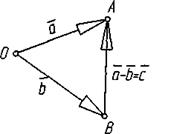 Множення вектора на число – це новий вектор
Множення вектора на число – це новий вектор 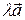 , довжина якого , довжина якого 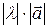 , а напрямок співпадає з напрямком , а напрямок співпадає з напрямком 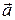 , при λ > 0 і протилежно спрямований при λ < 0.
Властивості: , при λ > 0 і протилежно спрямований при λ < 0.
Властивості:
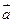
 1) 1) 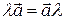 2)
2) 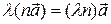 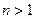
 3)
3) 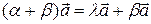 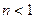
4)
5)
6)
| |||||||||
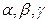 - координати - координати 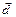 в базисі в базисі 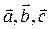 . .
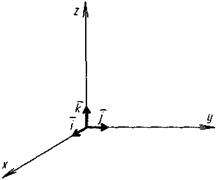 Вектори
Вектори 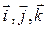 утворюють базис ортоспрямований. утворюють базис ортоспрямований.
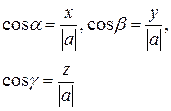
 Якщо вектор утворює з віссю ОХ кут φ, то проекція вектора на вісь – це добуток модуля вектора на
Якщо вектор утворює з віссю ОХ кут φ, то проекція вектора на вісь – це добуток модуля вектора на 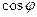 : :
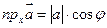
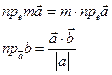 Властивості:
1. Рівні вектори мають рівні проекції на одну вісь:
Властивості:
1. Рівні вектори мають рівні проекції на одну вісь:
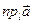 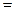 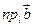 , якщо , якщо 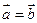 2. Проекція суми векторів дорівнює сумі проекцій векторів на цю вісь:
2. Проекція суми векторів дорівнює сумі проекцій векторів на цю вісь: 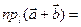 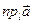  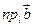 3.
3. 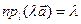 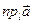 , де , де 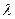 - дійсне число.
4. - дійсне число.
4. 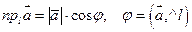 - гострий кут.
5. Проекція замкненої векторної лінії на вісь є нуль.
(2 і 3 – лінійні властивості проекції).
На площині - гострий кут.
5. Проекція замкненої векторної лінії на вісь є нуль.
(2 і 3 – лінійні властивості проекції).
На площині
 - довільний вектор площини,. - довільний вектор площини,.  = α = α 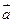 + β + β  -існує розкладання завжди. -існує розкладання завжди. 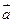 , ,  - не колінеарні вектори. - не колінеарні вектори.
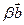
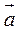 
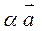
 Механічний сенс:
А = Fcosφ
Механічний сенс:
А = Fcosφ
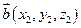

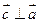 , , 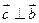
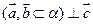
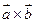 = = 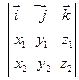 .
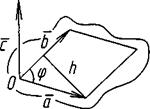
Механічний сенс – це момент вектора .
Механічний сенс – це момент вектора  відносно точкиА. відносно точкиА.
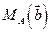 = = 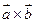
| Орти - одинічні вектори, спрямовані вздовж вісі координат 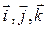 . Їх координати . Їх координати 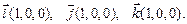 d можна розкласти по 3 некомпланарним векторам:
d можна розкласти по 3 некомпланарним векторам: 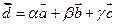 . .
 Кожний вектор Кожний вектор 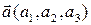 представлені у вигляді: представлені у вигляді: 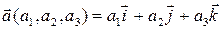 Проекція вектора на вісь – це довжина напрямленого відрізку прямої, кінці якого – основи перпендикулярів, що проведені із початка і кінця вектора на вісь координат, причому із знаком „+” або „-„ в залежності від того, гострий або тупий кут між віссю і вектором.
Кут між вектором і віссю (або між двома векторами) – найменший кут, на який треба повернути вектор, щоб його напрямок співпав з напрямком вісі.
прх(
Проекція вектора на вісь – це довжина напрямленого відрізку прямої, кінці якого – основи перпендикулярів, що проведені із початка і кінця вектора на вісь координат, причому із знаком „+” або „-„ в залежності від того, гострий або тупий кут між віссю і вектором.
Кут між вектором і віссю (або між двома векторами) – найменший кут, на який треба повернути вектор, щоб його напрямок співпав з напрямком вісі.
прх(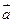 + +  ) = npx ) = npx 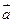 + npх + npх  aх =
aх = 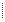 a a  cos cos  ау =
ау = 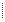 a a  cos cos  = = 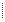 a a  sinα
ax + bx = х( sinα
ax + bx = х(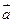 + +  ) - проекція суми векторів на кожну вісь дорівнює сумі проекцій вихідних векторів. ) - проекція суми векторів на кожну вісь дорівнює сумі проекцій вихідних векторів.
а = ах+ау +аг - диагональ пааллелепипеда,
Проекції вектора на вісі:
Радіус – вектор точки А – це вектор
Дата добавления: 2015-07-25; просмотров: 113 | Нарушение авторских прав
|