Поворот осей координат

В аналитической геометрии часто применяется преобразование координат, называемое поворотом осей. Оно заключается в следующем: обе оси координат поворачиваются в одну сторону на один и тот же угол, а начало координат остается неизменным. Примеры использования этого преобразования будут даны в следующих двух параграфах.

Пусть оси координат повернуты на угол (рис. 3.14). Угол – это угол, на который нужно повернуть старую ось до ее совмещения с новой осью ; угол считается положительным при повороте против часовой стрелки.

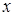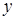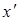Выведем формулы, позволяющие выразить старые координаты и любой точки через ее новые координаты и .

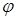Для этого построим радиус-вектор точки и обозначим через и 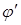углы, образованные им соответственно с осями и : точка имеет полярные координаты и 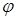, если за полярную ось принять ось , и координаты и 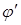, если за полярную ось принять ось .

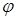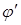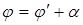Углы , и связаны равенством . Выражая декартовы координаты точки через ее полярные координаты, имеем:

(А)

(Б)

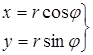
Заменяя в формулах 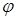(А) на и используя формулы для синуса и косинуса суммы двух углов, находим:

,

.

Отсюда, используя формулы (Б), находим следующие формулы, выражающие старые координаты 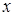и 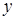через новые координаты 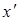и :

(3.42)

,

.

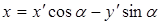Формулы обратного перехода, выражающие новые координаты через старые, мы получим аналогичным путем из формул (Б), заменяя в них угол 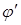на :

(3.42')

,

.

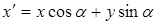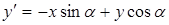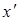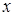Формулы (3.42') можно получить также из соотношений (3.42), рассматривая их как уравнения, определяющие и через и 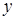, и разрешая их относительно 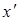и .

Формулы (3.42') можно было бы получить из формул (3.42) еще и следующим путем: поменять в формулах (3.42) местам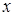и и 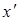, а также 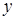и и заменить на (так как новые оси получаются из старых поворотом на угол , то и старые оси могут быть получены из новых поворотом в обратную сторону, т. е. на угол ).

Рекомендуем читателю получить формулы (3.42') этими двумя способами.

Дата добавления: 2015-07-11