|
Читайте также: |
Дана кривая: 
. Так как 
, то кривая – эллиптического типа.
По формуле (3.53) определяем угол поворота осей 
:
;
по тангенсу определяем 
:
.
Выберем в правой части знак минус (при этом будем иметь 
и сам угол острый). Теперь по 
находим 
и 
(в силу выбора угла они оба положительны):
,
.
Используя соотношение (3.42), записываем формулы преобразования координат:
,
.
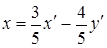Подставляя эти значения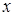 
и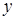 
в уравнение кривой, приводим его к виду:
.
После сокращения всех членов полученного уравнения на 5 находим:
.
Дополняем члены с 
и 
до полных квадратов:
,
откуда, деля все члены на 36, приходим окончательно к уравнению:
,
определяющему эллипс с полуосями 
и 
, центр которого по отношению к координатным осям 
и 
находится в точке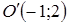 
и оси которого параллельны этим осям.
Расположение эллипса в старой и в новой системе координат представлено на рис. 3.17.
Дата добавления: 2015-07-11; просмотров: 133 | Нарушение авторских прав