Окружность.

Как известно, уравнение окружности радиуса 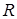с центром в точке имеет вид:

.

(3.1)

Если в этом уравнении раскрыть скобки и перенести в левую часть равенства, то уравнение примет вид:

	(3.1')

.

Геометрический смысл уравнения не изменится, если все его члены умножить на один и тот же, отличный от нуля и не зависящий от 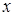и 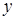множитель ; введем обозначения – , – , .

Уравнение (3.1') запишется тогда в виде:

	(3.2)
	(3.3)

.

Возникает вопрос: всякое ли уравнение вида (3.2) является уравнением некоторой окружности?

Чтобы ответить на этот вопрос, проделаем обратное преобразование уравнения (3.2) к виду (3.1), считая коэффициенты A, D, E и F произвольными (но ).

Разделим все члены уравнения (3.2) на А и введем обозначения: , , 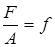; тогда уравнение (3.2) примет вид:

	(3.2')

.

Дополняя члены с x и y до полных квадратов и перенося член направо, придадим уравнению (3.2') вид:

.

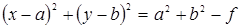Правая часть последнего уравнения может быть числом положительным, отрицательным или нулем.

1. Если , то положим .

Уравнение (3.3) запишется в виде:

	(3.3')

и является, как известно, уравнением окружности радиуса R с центром в точке .

2. Если , то уравнение (3.3) принимает вид:

	(3.3'')

.

Ему удовлетворяют только значения , (сумма двух квадратов может быть равна нулю только тогда, когда одновременно равен нулю каждый из них); таким образом, уравнению (3.3'') удовлетворяет единственная точка плоскости . Но, впрочем, можно говорить, что уравнение (3.3'') и в этом случае является уравнением окружности, но окружности, выродившейся в точку (окружности с нулевым радиусом).

3. Если , то полагая , приводим уравнение (3.3) к виду:

	(3.3''')

.

Поскольку сумма квадратов двух вещественных чисел не может быть числом отрицательным, то на плоскости xOy не существует точек, которые удовлетворяли бы уравнению (3.3'''). Поэтому уравнение (3.3''') не определяет никакой кривой; иногда говорят, впрочем, что уравнение (3.3''') является уравнением мнимой окружности.

Только учитывая это последнее замечание, можно говорить, что уравнение (3.2) всегда определяет окружность (вещественную, выродившуюся в точку или мнимую).

Дата добавления: 2015-07-11