Исследование общего уравнения кривой второго порядка

Наиболее общее уравнение второй степени относительно 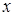и 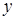имеет вид:

	(3.49)

.

В аналитической геометрии его называют общим уравнением кривой второго порядка. От уравнения:

уравнение (3.49) отличается наличием члена с произведением координат, т. е. коэффициент мы считаем не равным нулю.

В настоящем параграфе наша задача – показать, что и уравнение (3.49), так же, как и уравнение (3.39), может определять только одну из изученных нами ранее кривых – эллипс, гиперболу или параболу (с возможными для каждого из них случаями вырождения), найти способ по виду уравнения (3.49) установить тип определяемой им кривой (подобно тому, как это делалось для уравнения (3.39) по знаку произведения ) и научиться для каждого конкретного уравнения (3.49) строить кривую.

Наиболее простой способ решения этой задачи – при помощи поворота координатных осей на некоторый угол преобразовать уравнение (3.49) в уравнение вида (3.39) по отношению к новой системе координат, поскольку уравнение (3.39) нами уже изучено во всех подробностях.

Итак, повернем координатные оси на некоторый угол . Новые оси координат обозначим через и . Тогда старые координаты будут выражаться через новые по формулам (3.42) так:

,

.

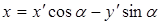Подставляя эти значения 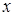и 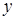в уравнение (3.49), после приведения подобных членов приведем его к виду:

(3.50)

Уравнение (3.50) имеет ту же структуру, что и уравнение (3.49). его можно записать в виде:

	(3.50')

где

(3.51)

(Значения новых коэффициентов и 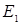, несущественные для дальнейшего, мы не описываем.)

Выберем теперь угол таким, чтобы новый коэффициент в уравнении (3.50') обратился бы в нуль; это дает нам для определения угла уравнение:

(3.52)

,

откуда находим:

(3.53)

.

Формула (3.53) определяет два значения угла , разность между которыми равна ; поэтому безразлично, какое из них выбрать: переход от одного к другому равносилен перестановке новых осей координат и .

После того, как угол определен по формуле (3.53), уравнение (3.50') приводится к виду:

	(3.54)

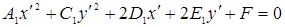
и, как нам известно, определяет эллипс (окружность), гиперболу или параболу (или вырождения этих кривых) в зависимости от знака произведения (см. § 3.6.).

В случае уравнения (3.54) этот вариант равен произведению , поскольку . Значит, , т. е. можно определить тип кривой второго порядка непосредственно по коэффициентам общего уравнения (3.49)

при кривая будет эллиптического типа (эллипс или окружность, точка, мнимый эллипс, мнимая окружность; при этом окружность мы будем иметь только при и );

при 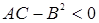– гиперболического типа (гипербола, пара пересекающихся прямых);

при – параболического типа (парабола или пара параллельных прямых – различных вещественных, совпавших или мнимых).

Инвариант , от знака которого, как мы видим, зависит тип кривой второго порядка, называют дискриминантом кривой.

Инвариант не единственный: другим инвариантом является сумма .

Итак, окончательный итог нашего исследования: существует только три типа кривых второго порядка (кривых в собственном смысле этого слова): эллипс (частным случаем которого является окружность), гипербола и парабола. Уравнение второй степени относительно 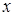и 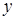не может определять на плоскости ничего другого, кроме этих кривых и перечисленных выше случаев распада и вырождения.

В заключении этой главы рассмотрим пример исследования и построения кривой второго порядка по ее уравнению вида (3.49).

Дата добавления: 2015-07-11