Примеры. Дополняем члены с и до полных квадратов и переносим свободный член в правую часть

1. ; .

Дополняем члены с 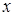и 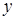до полных квадратов и переносим свободный член в правую часть равенства:

Деля на 16 приходим к уравнению эллипса:

(рекомендуется читателю самостоятельно построить кривые и найти координаты их фокусов в примерах 1, 4, 5, 8). Его центр ; полуоси , .

2. ; .

Это уравнение с помощью тех же преобразований, что и в примере 1, приводится к виду и определяет единственную точку .

3. ; .

Уравнение приводится к виду:

,

или

.

Это уравнение мнимого эллипса.

4. ; .

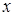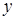Дополняя члены с и до полных квадратов, получаем:

.

Деля на 12, приходим к уравнению гиперболы:

.

Центр гиперболы – ; полуоси: вещественная , мнимая ; вещественная ось параллельна оси .

5. ; .

Уравнение преобразуется к виду:

.

Это уравнение гиперболы с центром в точке , с вещественной полуосью и мнимой ; вещественная ось гиперболы параллельна оси .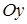

6. ; .

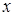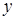После дополнения членов с и до полных квадратов приходим к уравнению:

.

Левая часть этого уравнения разлагается на множители и уравнение может быть записано в виде:

.

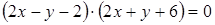Это уравнение определяет две пересекающиеся прямые: и .

7. ; .

Дополняя члены с 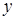до полного квадрата, приводим уравнение к виду:

.

Перенесем и свободный член в правую часть и вынесем в правой части за скобку коэффициент при 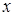(т. е. ):

.

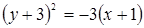Это уравнение параболы (3.38), где . Вершина параболы находится в точке , а осью симметрии служит прямая , параллельная оси ; парабола обращена в отрицательную сторону оси ; параметр параболы равен .

Для ее построения на чертеже полезно по исходному уравнению определить точки пересечения параболы с осями координат и использовать тот факт, что длина фокальной хорды параболы, перпендикулярной ее оси, равна (см. § 3.4).

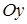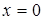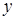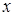В нашем случае с осью парабола не пересекается (при получаем для определения уравнение , имеющее комплексные корни), а ось она пересекает в точке (при для определения получаем уравнение , откуда ).

Фокус параболы находится в точке – на оси параболы, на расстоянии слева от ее вершины. Зная длину фокальной хорды и положение фокуса, можно определить еще две точки на нашей параболе: и . Использование всех этих данных дает нам возможность построить заданную параболу (рис. 3.13).

Директрисой этой параболы служит прямая 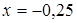, изображенная на чертеже пунктиром.

8. .

При помощи тех же преобразований, что и в предыдущем примере, приводим это уравнение к виду .

Это уравнение параболы (3.38'), где . Вершина параболы находится в точке ; осью параболы служит прямая , параллельная оси 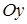; парабола обращена в положительную сторону оси .

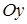9. .

Уравнение принадлежит к виду (3.39), но совсем не содержит одну из координат, а именно 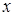. Являясь квадратным уравнением относительно 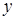, оно определяет два значения 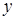: и ; таким образом, исходное уравнение в данном случае определяет две параллельные между собой и параллельные оси прямые.

Как мы уже указывали ранее, если бы в аналогичном случае (отсутствие одной из координат) корни уравнения были равными или комплексными, то соответствующее уравнение также определяло бы две параллельные прямые, но слившиеся в одну в первом случае и мнимые – во втором случае.

Например, уравнение определяет сдвоенную прямую 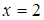, параллельную оси 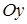; уравнение определяет две мнимые прямые:

и .

Рассмотренные нами ранее конкретные примеры 1-9 охватывают все возможные частные случаи, с которыми можно встретиться при преобразовании уравнения (3.39) к виду (3.36) – (3.38').

Дата добавления: 2015-07-11