Основы термодинамики

1. Теплоемкость идеального газа. Молярная теплоемкость. Удельная теплоемкость. Теплоемкости в различных процессах.

Примеры задач:

a. Фтор массой m = 35 г нагрели на 30 градусов, сообщив ему 415,5 Дж тепла, Найти молярную теплоемкость газа.

b. Молярная теплоемкость водорода равна 20,775 Дж/(моль•К). Найти его удельную теплоемкость.

2. Политропный процесс. Уравнение политропы.

Уравнение политропы: pVⁿ=const, где

Пример:
Молярная теплоемкость идеального двухатомного газа в некотором равновесном процессе равна 50 Дж/(моль•К). Найти показатель политропы.

3. Адиабатный процесс. Уравнение Пуассона.

, где

Пример:

При адиабатическом расширении кислорода массой 34 г газом совершена работа 300Дж. На сколько градусов понизилась температура газа? (в К)

4. Количество теплоты

Пример:

Если гелий массой m=3 г нагрели на 31 градусов, сообщив ему 249,3Дж. тепла, то молярная теплоемкость его равна (в Дж/(моль· К))

5. Работа в газовых процессах. Геометрический смысл работы.

Изобарный процесс:

Изохорный процесс:

A=0

Изотермический процесс:

Адиабатный процесс:

Пример:

Состояние некоторого разреженного газа изменилось из 1 в 3 (см.рис.). Найти работу газа.

Если состояние некоторого разреженного газа изменилось из 1 в 1 (см.рис.), то работа, совершенная при этом газом, равна (в Дж)

4 моля азота расширяются в 2,7 раза при постоянной температуре Т=300К. Работа расширения газа равна (в Дж)

6. Внутренняя энергия идеального газа

Пример:

На сколько изменится внутренняя энергия фтора массой 3 г при изменение его температуры на 20К (в Дж).

7. Изменение энтропии

Пример:

Найти изменение энтропии 10 кг воды (удельная теплоемкость воды 4190 Дж/кг К) при нагревании от 5^оС до 100 ^оС.

7 молей газа расширяются изотермически от объема V₁ = 2л до объема V₂ = 5,4л. Найти прирост энтропии системы (в Дж/К)

8. Связь изменения энтропии с термодинамической вероятностью

S = k ln(Ω), ΔS = k·ln(Ω₂/ Ω₁)

Пример:

Термодинамическая вероятность состояния системы уменьшилась в 5раз. Приращение энтропии системы равно (в Дж/К)

9. К.П.Д. циклического процесса.

Пример:
Тепловая машина с термическим коэффициентом полезного действия 33% отдает холодильнику 12 кДж тепла. Найти количество тепла, получаемого от нагревателя (в кДж)

Найти КПД циклов № 1, №2, №3, изображенных на рисунке.

10.

Цикл Карно. К.П.Д. цикла Карно.

Пример:

Температура нагревателя тепловой машины, работающей по циклу Карно, равна 330К, температура холодильника 296К. Найти коэффициент полезного действия машины.

11. Первое начало термодинамики.

Механические колебания

1.

Гармонические колебания. Параметры гармонических колебаний.

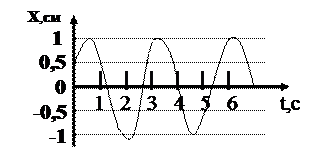x(t)=Asin(ωt+φ₀)

ω=2πν; ν=1/T

Пример:

Частица массой 10 г колеблется по закону Х=3 cos (32 t+ π/6) (см). Найти амплитуду ускорения частицы (в м/с²).

На рисунке представлен график синусоидальных колебаний. Найти начальную фаза колебаний в радианах. (Ответ – 0.524)

2.

Затухающие колебания. Добротность. Коэффициент затухания. Логарифмический декремент затухания.

Логарифмический декремент затухания:

θ=δ·T

Добротность:

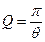
Пример:

Координата частицы массой 10г со временем изменяется по закону Х= 2е^{–0,01 t} cos(35t + π/6) (cм). Найти коэффициент сопротивления среды (в кг/с).

Координата частицы массой 20г со временем изменяется по закону
Х=2,4е^–0,1tcos(5t+π/6) (cм). Найти добротность и логарифмический декремент затухания системы.

Координата частицы массой 110г со временем изменяется по закону Х=3,4е^{–0,1 t} cos(10t + π/6) (cм). Сколько колебаний совершит система за время, когда амплитуда станет 2 см?

На рисунке представлен график затухающих колебаний. За какое время амплитуда колебаний уменьшилась в 2,71 раз (в с). Найти коэффициент затухания, добротность и логарифмический декремент затухания.

3. Вынужденные колебания. Амплитуда вынужденных колебаний.

Пример:

Тело массой 300 г совершает вынужденные колебания в установившемся режиме по закону (м). Найти амплитуду колебаний (в мм).

Тело массой 20 г совершает вынужденные колебания в установившемся режиме по закону 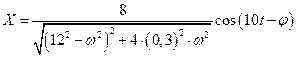(м). При какой круговой частоте наступит резонанс(в рад/с)?

4. Резонанс. Резонансная частота.

5. Пружинный маятник. Собственная частота пружинного маятника.

Пример:

Груз массой 300 г колеблется по закону Х= 1.6 cos (30 t +π/6) (см). Найти коэффициент жесткости пружины(в Н/м).

6. Математический маятник. Собственная частота математического маятника.

7. Физический маятник. Приведенная длинна.

Пример:

Приведенную длину физического маятника увеличили в 3 раза. Во сколько раз изменилась частота колебаний маятника?

Дата добавления: 2015-10-21