Механика твёрдого тела

1. Момент инерции системы материальных точек

Пример:

Два маленьких шара массами m₁ = 1кг и m₂= 2кг закреплены на тонком невесомом стержне длиной 1 м (см. рис.). Найти момент инерции системы относительно оси ОО'.

Из цилиндра радиусом R= 10см и массой М=500г вырезали середину радиусом r=5 см и массой m= 100 г. Найти момент инерции полученного кольца (в кг м²).

2. Стандартные формулы моментов инерции:

a. Момент инерции стержня относительно оси перпендикулярной стержню и проходящей через центр масс

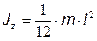
b. Момент инерции обруча или тонкостенного цилиндра относительно оси, проходящей через центр масс и параллельно оси

c. Момент инерции однородного диска или сплошного однородного цилиндра относительно оси, проходящей через центр масс и параллельно оси

d. Момент инерции однородного шара относительно оси, проходящей через центр масс

e. Момент инерции материальной точки

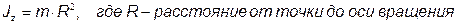
3. Теорема Штейнера

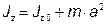
Пример:

Найти момент инерции вала радиусом 5см и массой 39кг относительно оси АА' (в кг^.м²).

4. Основное уравнение динамики вращательного движения для тела закрепленного на неподвижной оси.

Пример:

Вал радиусом 2см и массой 200кг вращается вокруг своей оси. Суммарный момент внешних сил равен 3 Н•м. Угловое ускорение вала равно (в рад/с²)

5. Кинетическая энергия тела, совершающего плоское движение

Т = Т_вр+Т_пост, где Т_вр –энергия вращательного движения, Т_пост - энергия поступательного движения

Пример

Сплошной цилиндр массой 20кг и радиусом 10см катится без проскальзывания по горизонтальной поверхности со скоростью 2 м/с. Найти отношение его кинетической энергии поступательного движения центра масс к кинетической энергии вращения, кинетическую энергию тела.

6. Момент силы относительно точки

Пример:

В плоскости YZ на материальную точку с координатами y = 1м и z = 2.5м под прямым углом к радиус-вектору точки действует cила 3 Н. Момент этой силы относительно точки О равен (в Н^.м)

Колесо вращается так, как показано на рисунке белой стрелкой. К ободу колеса приложена сила, направленная по касательной. Какие вектора правильно изображают: момент импульса колеса, угловую скорость колеса.

1. Момент импульса материальной точки. Направление момента импульса.
   
   
   
   Пример:
   
   По окружности с радиусом 3м и с центром в начале координат в плоскости YZ со скоростью 1м/с движется частица массой 9кг. Найти момент импульса этой частицы относительно точки О(в кг•м²/с).
   
   

8. Момент импульса тела относительно оси. Направление момента импульса.

Дата добавления: 2015-10-21