Гироскопический эффект. Пусть гироскоп имеет только две степени свободы: поворот вокруг оси и вместе с

Пусть гироскоп имеет только две степени свободы: поворот вокруг оси и вместе с кольцом 2 - вокруг оси (двухстепенной гироскоп). В этом случае, если толкнуть кольцо 2, то оно начнет свободно вращаться вокруг оси , в то время как трехстепенной гироскоп на такие толчки практически не реагирует. Не реагирует трехстепенной гироскоп и на вращение основания, сохраняя неизменным направление своей оси .

Рис. 4

Пусть основание 1 вращается вокруг оси (или любой параллельной ей оси) с угловой скоростью ( 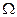>> ). Вращаясь вместе с основанием гироскоп совершает вынужденную прецессию вокруг оси . Согласно уравнению (2) на ротор 3 должен действовать момент , который, очевидно, могут создать только силы , давления подшипников , на ось ротора. Так как центр масс ротора 3 неподвижен, то по теореме о движении центра масс (, где - равнодействующая всех внешних сил, действующих на данную систему) должно быть , и, следовательно, силы , образуют пару.

Но когда подшипники действуют на ось ротора с силами , , то по третьему закону динамики (две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны) ось будет одновременно действовать на подшипники , с такими же по модулю и противоположными по направлению силами , .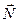

Пара сил 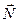, называется гироскопической парой, а её момент - моментом гироскопической пары или гироскопическим моментом (моментом гироскопической реакции).

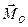Поскольку момент противоположен (), то:

и . (4)

Правило Н.Е. Жуковского: если быстро вращающемуся гироскопу сообщить вынужденное прецессионное движение, то на подшипники, в которых закреплена ось ротора гироскопа, начнет действовать гироскопическая пара с моментом , стремящаяся кратчайшим путем установить ось ротора параллельно оси прецессии так, чтобы направления векторов 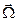и совпали.

Под действием гироскопической пары кольцо 2 начнет вращаться с ротором вокруг оси ; при этом угол , а с ним и момент будут убывать, и когда станет , вращение кольца 2 прекратится.

Уравновешенный гироскоп можно реализовать, например, поместив гироскоп в карданов подвес (о чем упоминалось выше).

Карданов подвес - универсальная шарнирная опора, позволяющая закреплённому в ней объекту вращаться одновременно в нескольких плоскостях. Основная идея карданова подвеса: несколько колец, расположенных одно внутри другого, соединяются в двух противоположных точках, что дает им возможность вращаться относительно друг друга. Если в центре колец поместить груз, то он будет сохранять вертикальное положение. Какие бы движения ни совершали кольца, груз останется неподвижной, поскольку кольца гасят колебания.

Т.е., если в кардановом подвесе закрепить вращающееся тело, то оно будет сохранять направление оси вращения независимо от ориентации самого подвеса. Карданов подвес обеспечивает вращающемуся телу свободный поворот в пространстве вокруг трех взаимно перпендикулярных осей, пересекающихся в одной точке, называемой точкой подвеса. Эта точка при любых указанных поворотах остается неподвижной (рис. 5).

Рис. 5

Будем обозначать в дальнейшем вектор главного кинетического момента гироскопа через (ранее обозначался - ). Внешний момент будем обозначать (ранее обозначался - ).

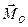Сформулируем основные правила для проявления гироскопических эффектов.

Дата добавления: 2015-10-21