
Читайте также:
|
При выполнении предыдущих контрольных работ мы столкнулись с тем, что ряд физических и геометрических задач сводится к нахождению производных от функций. Наряду с этим ряд задач сводится к обратной операции–отысканию функции по ее производной. Эта операция называется интегрированием, следовательно, интегрирование должно заключаться в следующем: задана производная –требуется найти функцию.
Определение. Функцию  , заданную на промежутке
, заданную на промежутке 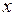 , называют первообразной для функции
, называют первообразной для функции  , заданной на том же промежутке, если для всех
, заданной на том же промежутке, если для всех  выполняется равенство
выполняется равенство 
 (или, что то же самое, равенство
(или, что то же самое, равенство  ). Например, для функции
). Например, для функции  первообразной будет функция
первообразной будет функция  , т. к.
, т. к.  для всех
для всех  ; для функции
; для функции  первообразной будет функция
первообразной будет функция  , т.к.
, т.к.  для всех
для всех  ; для скорости
; для скорости  точки первообразной будет путь
точки первообразной будет путь  , который прошла эта точка, т. к.
, который прошла эта точка, т. к.  , и так далее.
, и так далее.
Так как первообразная имеет производную, следовательно, она непрерывна. Но верно и более глубокое утверждение: если функция  непрерывна, то
непрерывна, то  она имеет первообразную. В интегральном исчислении мы будем иметь дело только с непрерывными функциями.
она имеет первообразную. В интегральном исчислении мы будем иметь дело только с непрерывными функциями.
Если функция  является первообразной для функции
является первообразной для функции  на промежутке
на промежутке  , то и любая из функций вида
, то и любая из функций вида  является первообразной для
является первообразной для  на том же промежутке. Это следует из того, что
на том же промежутке. Это следует из того, что
 .
.
Нетрудно убедиться в верности и обратного утверждения: если  есть первообразная
есть первообразная  , то все первообразные для
, то все первообразные для  содержатся в формуле
содержатся в формуле  .
.
Определение. Совокупность всех первообразных для заданной функции  на промежутке
на промежутке  называется неопределенным интегралом этой функции и обозначается так:
называется неопределенным интегралом этой функции и обозначается так:  (читается: ”интеграл эф от икс дэ икс”);
(читается: ”интеграл эф от икс дэ икс”);
q  называется подынтегральной функцией;
называется подынтегральной функцией;
q произведение  – подынтегральным выражением;
– подынтегральным выражением;
q  знаком интеграла;
знаком интеграла;
q  – переменной интегрирования.
– переменной интегрирования.
Если  есть первообразная для
есть первообразная для  , то
, то  (C –произвольная константа). Например,
(C –произвольная константа). Например, 

Из определения интеграла следует, что каждой формуле дифференциального исчисления  соответствует формула
соответствует формула  в интегральном исчислении, так что в частности вся таблица производных может быть переписана в виде таблицы интегралов:
в интегральном исчислении, так что в частности вся таблица производных может быть переписана в виде таблицы интегралов:
I.  где
где  ; II.
; II. 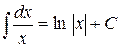 ;
;
III.  ; IV.
; IV.  ;
;
V.  ; VI.
; VI.  ;
;
VII.  ; VIII.
; VIII.  ;
;
IX.  ; X.
; X.  ;
;
XI.  ; XII.
; XII.  ;
;
XIII.  ; XIV.
; XIV.  ;
;
XV.  XVI.
XVI.  .
.
Займемся теперь основными свойствами неопределенных интегралов и правилами их вычисления.
Примем без доказательства свойства неопределенного интеграла:
1. 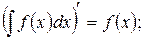
2. 
3. 
4.  ;
;
5.  (k –постоянная);
(k –постоянная);
6.  .
.
Дата добавления: 2015-10-21; просмотров: 97 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задание 3. Некоторые квантовомеханические системы. Тепловое излучение | | | Интегрирование подстановкой |