Определенный интеграл и его геометрический смысл

Пусть функция является первообразной для функции в некотором промежутке X, а числа 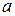и принадлежат этому промежутку.

Определение. Приращение любой из первообразных функций при изменении аргумента от до называется определенным интегралом от 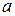до функции и обозначается .

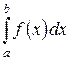Числа 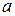и называются пределами интегрирования: нижним, верхним. Отрезок называется отрезком интегрирования. Функция называется подынтегральнойфункцией, а переменная переменной интегрирования. Таким образом, по определению,

(2.4)

Равенство (2.1) называется формулой Ньютона-Лейбница.

Существует и другой подход к введению понятия определенного интеграла, основанный на рассмотрении пределов интегральных сумм, который в большей степени приспособлен для приложений. Рассмотрим его на примере вычисления площади криволинейной трапеции.

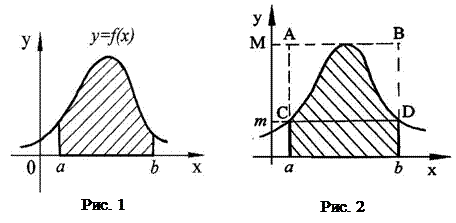Пусть дана фигура, ограниченная графиком непрерывной и неотрицательной функции , отрезком и прямыми ; (рис. 1). Такую фигуру называют криволинейной трапецией. Найдем ее площадь.

Заметим, что на отрезке можно указать такую точку , что площадь криволинейной трапеции равна

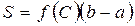. (2.5)

Действительно, пусть 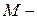наибольшее значение функции на отрезке , а наименьшее. Проведем прямые 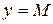и . Тогда криволинейная трапеция целиком содержится в прямоугольнике и содержит целиком прямоугольник (рис. 2).

Поэтому или , т.к. ; 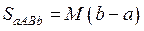. Возьмем число и .

На отрезке возьмем такую точку , что . Так как функция непрерывна на , то каждому значению функции 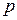соответствует хотя бы одно значение ее аргумента , лежащего внутри отрезка . Тогда . Данное свойство называется теоремой о среднем.

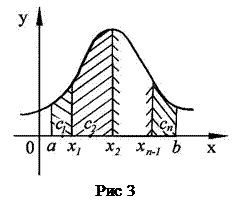Найдем теперь площадь криволинейной трапеции через определенный интеграл. Разобьем криволинейную трапецию на полос так, как показано на рис. 3. При этом на отрезке появились точки , ,..., .

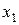В соответствии с формулой (2.5) найдем для первой полосы точку , такую, что площадь первой полосы равна 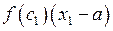. Для второй полосы найдем точку 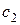, такую, что площадь полосы равна . Поступаем так для всех полос, т.к. площадь криволинейной трапеции равна сумме площадей полос, на которую она разбита:

.

Такого типа равенство будет иметь место, как бы мы не разбивали криволинейную трапецию на полосы. Длину наибольшего из отрезков обозначим через . Перейдем в нем к пределу при 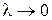, получим

.

Обозначим

,

через выражение получим

. (2.6)

Таким образом, ввели определенный интеграл через предел особого рода сумм (интегральных сумм).

Определение. Пусть дана функция , определенная на отрезке , где 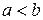. Выполним следующие операции:

1.Разобьем отрезок на частей точками , так что .

2.Величину 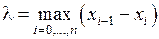назовем шагом разбиения.

3.На каждом из отрезков зафиксируем произвольную точку , .

4.Составим сумму всех произведений , ; или в сокращенном виде

, (2.7)

где .

Суммы вида (1.7) называются интегральными суммами функции .

Очевидно, что при различных разбиениях отрезка на части получим различные интегральные суммы вида (2.4). Таким образом, для данной функции и данного отрезка можно составить бесконечное множество интегральных сумм вида (2.4), которые зависят от числа и от выбора точек деления и точек . В примере вычисления площади криволинейной трапеции точки подбирались специально, что не противоречит определению определенного интеграла через пределы интегральных сумм.

Определение. Если при любой последовательности разбиений отрезка таких, что , при любом выборе точек интегральная сумма стремится к одному и тому же конечному числу : , то число называется определенным интегралом от функции на отрезке и обозначается . Итак, по определению,

. (2.8)

Заметим без доказательств, что предел в правой части равенства (2.8) существует и конечен, если непрерывна на отрезке .

Если непрерывна и неотрицательна, то определенный интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции , осью абсцисс и прямыми ; (см. рис. 1), т.е.

. (2.9)

В этом заключается геометрический смысл определенного интеграла. Без доказательства заметим, что оба определения эквивалентны. Второе определение помогает получить приложение определенного интеграла (вычисление площади и т.д.), а формула Ньютона - Лейбница позволяет вычислить определенный интеграл без вычисления предела интегральной суммы.

Пример 4. Вычислить .

Решение. Используя правила 1 и 2, представим определенный интеграл в виде суммы трех более простых интегралов, к каждому из которых применим формулу Ньютона-Лейбница:

.

Пример 5. Вычислить .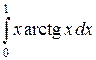

Решение. Положим ; 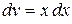, тогда

, .

Следовательно,

.

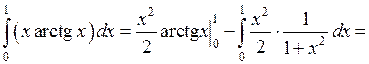
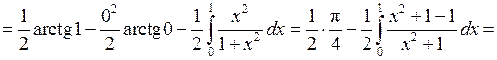
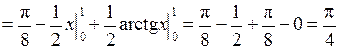Пример 6. Вычислить .

Решение. Сделаем замену , тогда ; ; ; . Новые пределы интегрирования находим из соотношения ; если , то 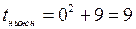; если , то .

Поэтому

---

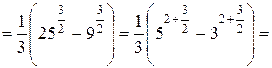
Дата добавления: 2015-10-21