
|
Читайте также: |
Замена переменной (подстановка) 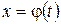 в интеграл производится по формуле
в интеграл производится по формуле
 ; (1.1)
; (1.1)
при этом говорят, что в интеграле слева сделана замена переменной (подстановка) 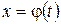 . Формулой (1.1) можно пользоваться следующим образом: подобрать функцию
. Формулой (1.1) можно пользоваться следующим образом: подобрать функцию 
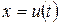 так, чтобы, подставив вместо
так, чтобы, подставив вместо  подынтегральное выражение, получить более простой интеграл.
подынтегральное выражение, получить более простой интеграл.
Пример 1. Найти 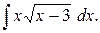
Решение. С целью упрощения подынтегрального выражения положим 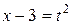
 . Отсюда
. Отсюда 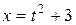 ;
; 

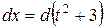 ;
; 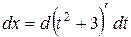 ;
; 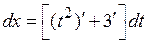 ;
;  ;
;  . Заменив всюду под интегралом
. Заменив всюду под интегралом  на
на  , получим
, получим
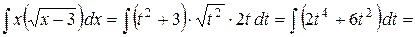
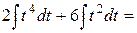

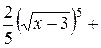

При вычислении воспользовались формулой 
Пример 2. Найти 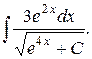
Решение. Заметим, что  Целесообразно ввести переменную
Целесообразно ввести переменную  . Тогда
. Тогда  ;
; 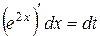 ;
;  . Заменив всюду под интегралом
. Заменив всюду под интегралом 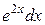 на
на 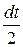 ,
,  на
на  , получим
, получим
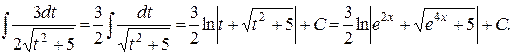
Пример 3. Найти 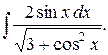
Решение. Заметим, что 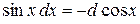 , т.к.
, т.к.
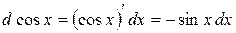 . Целесообразно ввести переменную
. Целесообразно ввести переменную 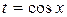 . Заменив всюду под интегралом
. Заменив всюду под интегралом  на
на 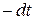 ,
,  на
на  , получим
, получим
 Пример 4. Найти
Пример 4. Найти 
Решение. Заметим, что 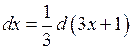 , т.к.
, т.к. 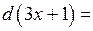
 . Целесообразно ввести переменную
. Целесообразно ввести переменную  . Тогда
. Тогда 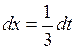 . Заменив всюду под интегралом
. Заменив всюду под интегралом  на
на 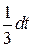 ,
,  на
на  ; получим
; получим
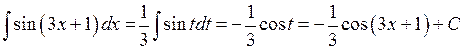 .
.
На основании вышеизложенного можно ввести формулу
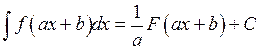 , (1.2)
, (1.2)
где 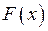 – первообразная функции
– первообразная функции  .
.
Тогда 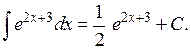
Из формулы (1.2) получим
1. 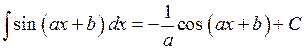 .
.
2.  .
.
3.  .
.
Дата добавления: 2015-10-21; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Первообразная и неопределенный интеграл | | | Интегрирование по частям |