
|
Читайте также: |
Рациональной дробью называется функция R (х), представленная в виде
 ,
,
где Р (х) и Q (х) – многочлены с действительными коэффициентами.
Рациональная дробь R (x) называется правильной, если степень числителя меньше степени знаменателя.
Всякая правильная рациональная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех типов:
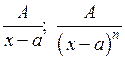 (n > 1 натуральное число);
(n > 1 натуральное число);
 (n > 1 натуральное число),
(n > 1 натуральное число),
где  , т. е. корни знаменателя мнимые.
, т. е. корни знаменателя мнимые.
Таким образом, для интегрирования правильных рациональных дробей достаточно уметь: 1) интегрировать простейшие дроби; 2) разлагать рациональные дроби на простейшие.
Пример 1.  .
.
Решение. Заметим, что  , т.к.
, т.к.  .
.

Пример 2.  .
.
Решение. 

Для интегрирования простейших дробей третьего вида  вычисляют, используя замену переменных
вычисляют, используя замену переменных  , откуда
, откуда  ;
; 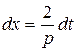 .
.
Пример 3. Найти  .
.
Решение. Сделаем замену переменных 
 ;
;  ;
;  ;
;  ;
;  .
.
Заменив всюду под интегралом  на
на  ,
,  на
на  , получим
, получим

При вычислении воспользовались формулой  . Второй из полученных интегралов является табличным, а первый находим подстановкой
. Второй из полученных интегралов является табличным, а первый находим подстановкой  , откуда
, откуда  ;
;  ;
;  ;
;  . Следовательно,
. Следовательно,
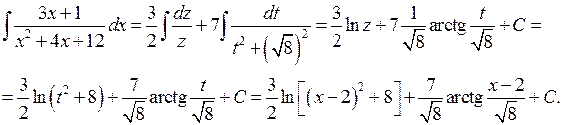
Задача 1. Вычислить интегралы:
1)

Можно проверить, что интеграл найден верно. Для этого воспользуемся формулой 

Ответ:  .
.
2)

Ответ: 
3)
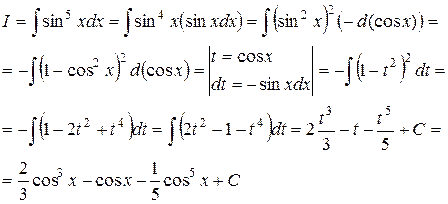
Ответ:  .
.
Так находятся интегралы, если есть хотя бы одна нечетная степень  и
и  В случае, если имеются только четные степени, интегралы находят с помощью понижения степени по формулам тригонометрии.
В случае, если имеются только четные степени, интегралы находят с помощью понижения степени по формулам тригонометрии.
4)

Ответ: 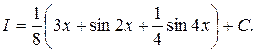
5)

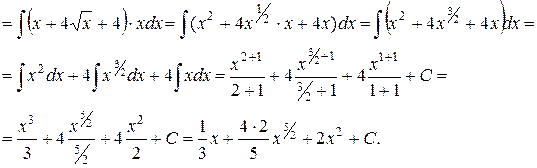
Ответ: 
6)


Ответ: 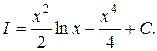
7)

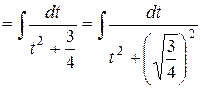

Ответ: 2)
Контрольные варианты к задаче 1.
ЗАДАНИЕ. Вычислить неопределенные интегралы:
1. 1)  , 2)
, 2)  , 3)
, 3)  ,
,
4) 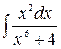 , 5)
, 5)  , 6)
, 6)  , 7)
, 7)  .
.
2. 1)  , 2)
, 2)  , 3)
, 3) 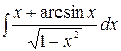 ,
,
4)  , 5)
, 5)  , 6)
, 6)  7)
7)  ,
,
3. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
4. 1)  , 2)
, 2) 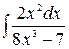 , 3)
, 3)  ,,4)
,,4) 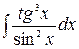 , 5)
, 5) 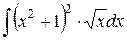 , 6)
, 6)  , 7)
, 7)  .
.
5. 1) 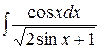 , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  7)
7)  .
.
6. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
7. 1)  , 2)
, 2) 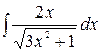 , 3)
, 3) 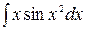 , 4)
, 4)  ,
,
5)  6)
6) 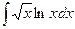 7)
7)  .
.
8. 1)  , 2)
, 2)  3)
3)  , 4)
, 4) 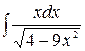 ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
9. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
10. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
11. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
12. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5) 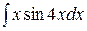 , 6)
, 6)  , 7)
, 7)  .
.
13. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7)  .
.
14. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6)  , 7)
, 7) 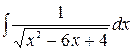 .
.
15. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  ,
,
5)  , 6)
, 6) 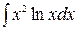 , 7)
, 7) 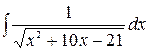 .
.
16. 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , 6)
, 6)  , 7)
, 7)  .
.
Дата добавления: 2015-10-21; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование по частям | | | Определенный интеграл и его геометрический смысл |