|
Читайте также: |
Непрерывный сигнал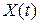 
, принимает бесконечное множество возможных значений на интервале 
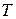. Вероятность появления конкретного значения 
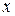, бесконечно мала, вследствие бесконечного количества их возможных значений. Пусть 
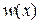– плотность вероятности сигнала 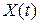на интервале .
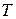Для получения значения энтропии сигнала 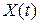разделим область изменения сигнала 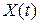на 
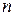интервалов с равномерным шагом 
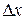(см. рис. 7.1). Вероятность нахождения сигнала в интервале от 
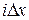до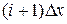 
соответственно будет равна 
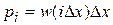. В случае если рассмотреть дискретный источник, где в качестве сообщения будем рассматривать факт нахождения значения 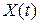на интервале 
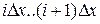, то по (7.__) энтропия источника непрерывных сообщений будет равна
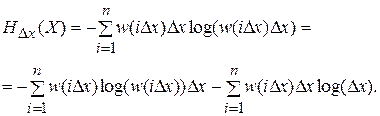(7.1)
При переходе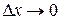 
и так как 
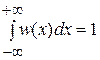, получим
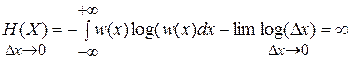. (7.2)
Таким образом, энтропия непрерывного источника сообщений равна бесконечности.
Первую часть выражения (2.26) можно рассматривать как дифференциальную энтропию непрерывного источника сообщений:
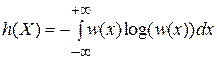. (7.3)
Значение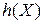 
показывает степень неопределенности различных процессов. Исходя из (2.27) значение дифференциальной энтропии может быть 
.
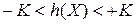Максимальное значение 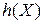достигается при нормальном распределении сигнала 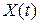[]. Для 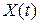с дисперсией 
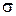значение
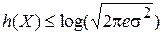. (7.4)
Дата добавления: 2015-10-21; просмотров: 80 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лабораторная работа №6. Типичные и нетипичные комбинации источника дискретных сообщений | | | Лабораторная работа №7. Линейные коды |