
|
Читайте также: |
В лабораторной работе исследуется энтропия источника дискретных сообщений без памяти и двоичного кодирующего устройства на основе кода Windows 1251. Схема исследуемого устройства приведена на рис. 4.1.

Рис. 4.1. Схема лабораторной работы
Мера информации содержащийся в сообщении 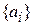 оценивается как:
оценивается как:
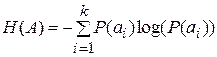 .
.
Максимальное значение 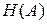 будет принимать если
будет принимать если 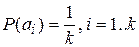 , в этом случае
, в этом случае
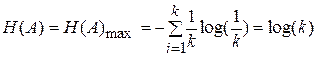 (2.11)
(2.11)
Для источника дискретных сообщений вводится понятие избыточности источника:
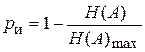 , (2.12)
, (2.12)
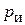 является безразмерной величиной в пределах [0..1].
является безразмерной величиной в пределах [0..1].
Для определения предельных характеристик дискретных каналов связи К.Шенноном была введена была введена величина названная пропускной способностью канала связи 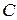
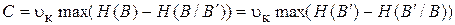 . (2.24)
. (2.24)
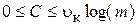
При полностью независимых входе и выходе канала связи (канал связи полностью забит помехами) 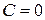 . Максимальное значение
. Максимальное значение 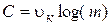 , получается если в канале связи нет помех
, получается если в канале связи нет помех 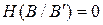 и
и 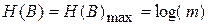 .
.
Например, в случае двоичного дискретного канала связи (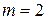 ), при заданной вероятности ошибки в канале
), при заданной вероятности ошибки в канале 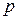 , пропускная способность будет равна
, пропускная способность будет равна
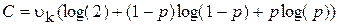 .
.
График нормированной пропускной способности канала связи представлен на рис. 4.2.
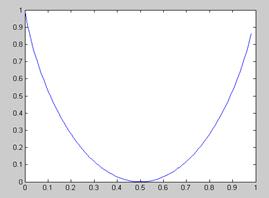 Рис. 4.2. График зависимости нормированной пропускной способности двоичного дискретного канала связи от вероятности ошибки в канале связи
Рис. 4.2. График зависимости нормированной пропускной способности двоичного дискретного канала связи от вероятности ошибки в канале связи
| Из рис. 4.2 видно что пропускная способность канала связи максимальная в случае если ошибок в канале связи нет 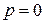 , или в случае если , или в случае если 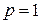 , то есть каждый передаваемый символ меняется на противоположное значение (фактически канал связи работает в качестве инвертора). Если , то есть каждый передаваемый символ меняется на противоположное значение (фактически канал связи работает в качестве инвертора). Если 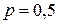 – вероятность приема символа не зависит от того какой символ передает источник сообщения и в этом случае пропускная способность канала связи – вероятность приема символа не зависит от того какой символ передает источник сообщения и в этом случае пропускная способность канала связи 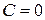 . .
|
Дата добавления: 2015-10-21; просмотров: 152 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Лабораторная работа №3. Импульсные виды модуляции | | | Этап II |