Лабораторная работа №7. Линейные коды

В лабораторной работе исследуются линейные коды, получившие большое распространение на практике. Линейным двоичным кодом называется код, для которых сумма по модулю два любых разрешенных кодовых комбинаций является разрешенной кодовой комбинацией.

Линейный код является систематическим, если 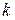символов его являются информационными, а символов являются проверочными (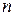 – длинна кодовой последовательности).

Линейный код обозначают 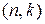и его можно записать как:

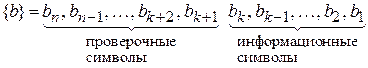
Избыточность линейного кода определяется как:

.

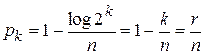Для примера рассмотрим код (8,4), проверочные символы которого формируются следующим образом:

.

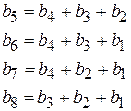Например, при передачи символа 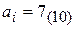, кодовая последовательность будет имеет значение: .

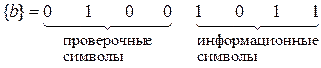Получатель сообщения примет последовательность 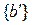. Вследствие ошибки в канале принятая последовательность может отличатся от переданной последовательности: 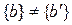. В этом случае выбирается комбинация наиболее близкая по расстоянию по Хеменгу из числа всех возможных комбинациях.

Например, при передаче рассмотренной выше последовательности возникли ошибки, результаты сравнения приведены в табл.7.1.

Табл. 7.1. Пример работы линейного кода (8,4)

Переданная последовательность	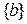0 1 0 0 1 0 1 1	0 1 0 0 1 0 1 1	0 1 0 0 1 0 1 1
Ошибка	0 0 0 0 0 0 0 0	0 0 0 0 0 0 0 1	1 0 0 0 0 0 0 1
Принятая последовательность	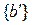0 1 0 0 1 0 1 1	0 1 0 0 1 0 1 0	1 1 0 0 1 0 1 0
Все возможнее комбинации кода	Расстояние по Хеменгу между переданной и принятой последовательностью
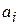
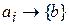
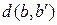
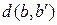
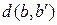
	0 0 0 0 0 0 0 0
	0 1 1 1 1 0 0 0
	1 0 1 1 0 1 0 0
	1 1 0 0 1 1 0 0
	1 1 0 1 0 0 1 0
	1 0 1 0 1 0 1 0
	0 1 1 0 0 1 1 0
	0 0 0 1 1 1 1 0
	1 1 1 0 0 0 0 1
	1 0 0 1 1 0 0 1
	0 1 0 1 0 1 0 1
	0 0 1 0 1 1 0 1
	0 0 1 1 0 0 1 1
	0 1 0 0 1 0 1 1
	1 0 0 0 0 1 1 1
	1 1 1 1 1 1 1 1
Декодирование	Верно	Верно	Невозможно

При реализации декодера все возможные комбинации кода записываются в ПЗУ. Формируемые полиномы в кодере, так же обычно представляются в виде двоичной матрицы. Для рассмотренного примера эта матрица имеет значение:

.

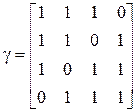Процесс кодирования в этом случае выглядит следующим образом:

.

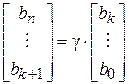К недостаткам линейных кодов можно отнести необходимость хранения больших массивов чисел.

Дата добавления: 2015-10-21