Анализ работы источника постоянного тока.

Согласно закону Ома, сила тока в замкнутой цепи, определяется по формуле (3.4).

Полезная мощность – это мощность, выделяемая во внешней цепи и она равна:

, (6.1)

где U₁ – падение напряжения во внешней цепи.

Мощность, выделяемая внутри источника равна

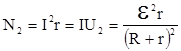, (6.2)

где U₂ – падение напряжения внутри источника тока.

Полная мощность

. (6.3)

Чтобы найти, при каком внешнем сопротивлении выделяется наибольшая полезная мощность N₁, возьмем производную по R от выражения (6.1) и приравняем ее к нулю.

Поскольку e ¹ 0, то r – R = 0 т.е. R = r. Следовательно, при R = r функция (6.1) имеет экстремум.

Исследуем знак производной для точек, соответствующих R < r и R > r. Очевидно, что в первом случае , во втором . Функция в данной точке имеет максимум. Это означает, что при R = r полезная мощность максимальна и ее значение

.

Коэффициент полезного действия источника постоянного тока равен:

. (6.4)

При R = r h = 0,5

С увеличением R КПД источника тока увеличивается.

Вопросы для обсуждения:

1. Что называется электрическим током?

2. Сформулируйте условия необходимые для существования тока проводимости.

3. Дайте определение силы тока, плотности тока.

4. Какая существует зависимость между плотностью тока и средней скоростью направленного движения носителей тока?

5. Что такое электродвижущая сила, напряжение?

6. Закон Ома в интегральной форме.

7. Закон Ома в дифференциальной форме.

8. Закон Джоуля-Ленца в интегральной форме.

9. Полезная мощность, мощность, выделяющаяся внутри источника, полная мощность и КПД источника постоянного тока.

10. Приведите примеры применения источников постоянного тока.

Литература

1. Савельев И.В. Курс общей физики: В 3 т. Т.2. – М.: Наука, 1988.

2. Савельев И.В. Курс общей физики: В 5 кн. Кн.2. – М.: Изд-во «Астрень АСТ», 2002.

3. Наркевич И.И., Волмянский Э.И., Лобко С.И. Физика для втузов. В 2 т. Т. 2. – Мн.: Вышэйшая школа, 1994.

4. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 2001-2002.

Дата добавления: 2015-10-21