Задание.

ЛАБОРАТОРНАЯ РАБОТА №1.

СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НОРМАЛЬНОЙ ПЕРЕГРУЗКОЙ И УГЛОМ ТАНГАЖА САМОЛЕТА.

Цель работы: синтез систем и изучение процессов автоматического управления нормальной перегрузкой и углом тангажа самолета.

ЗАДАНИЕ.

За невозмущенное движение принимается горизонтальный полёт с постоянной скоростью. Линеаризованные уравнения продольного движения самолёта при этом имеют вид (при отсутствии ветра):

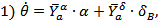
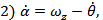
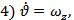
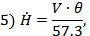
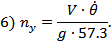
Обозначения:

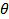– угол наклона траектории,

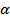– угол атаки,

– угол отклонения рулей высоты,

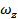– угловая скорость вращения корпуса самолета,

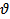– угол тангажа,

– высота полёта,

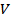– скорость полёта,

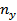– нормальная перегрузка.

Вариант высоты № 3, вариант числа маха № 6. Режим полёта:

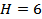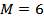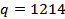, , , V .

Динамические коэффициенты:

, , ,

, , .

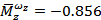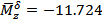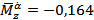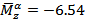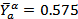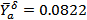1. ДИНАМИКА САМОЛЁТА.

По дифференциальным уравнениям продольного движения составим структурную схему в системе Simulink.

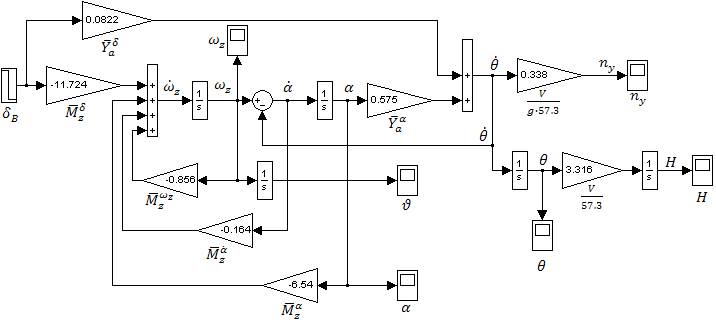
Рис. 1. Структурная схема, описывающая динамику самолёта.

Без учёта сил руля высоты () выведем передаточные функции самолёта по углу атаки, по перегрузке, по углу наклона траектории, по угловой скорости, по углу тангажа и по высоте от угла отклонения рулей высоты.

Из уравнения (1):

7)

Подставим выражение (7) в уравнение (2):

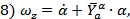
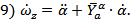
Подставим выражения (8) и (9) в уравнение (3):

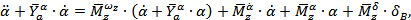
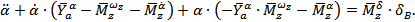
Сделаем преобразование Лапласа для последнего выражения:

Выразим :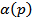

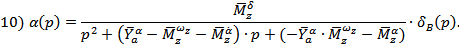
Введем условные обозначения:

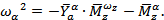
Выражение (10) примет вид:

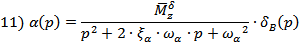
Подставим выражение (7) в уравнение (6):

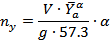
Сделаем преобразование Лапласа последнего выражения и подставим в него :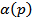

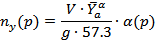
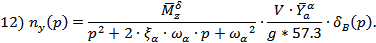
Преобразуем по Лапласу выражение (7):

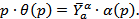
Подставим в него выражение (11) и выразим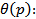

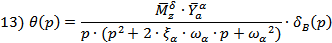
Выразим из выражения (2) 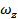и преобразуем его по Лапласу:

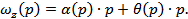
Подставим в последнее уравнение выражения (11) и (13):

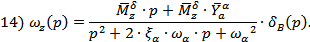
Преобразуем по Лапласу уравнение (4):

Выразим из последнего выражения и подставим в него выражение (14):

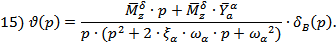
Преобразуем по Лапласу уравнение (5):

Выразим из последнего выражения и подставим в него выражение (13):

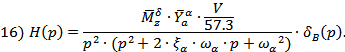
Из уравнений (11), (12), (13), (14), (15), (16) получим передаточные функции:

· по углу атаки α

· по нормальной перегрузке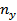

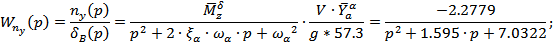
· по углу наклона траектории θ

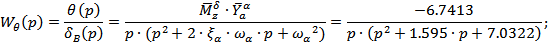
· по угловой скорости вращения корпуса самолета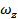

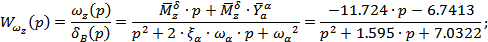
· по углу тангажа ϑ

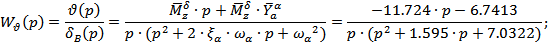
· по высоте H

Исследуя передаточные функции, проанализируем характеристики устойчивости и управляемости самолёта.

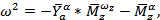
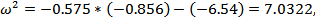
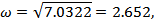
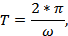
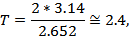
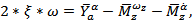
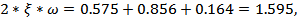
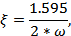
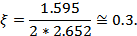
При декременте затухания 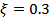величина перерегулирования 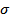будет равна

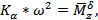
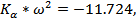
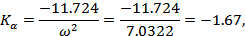
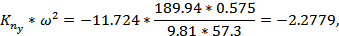
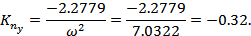
Итак, динамические характеристики управляемости:

Статические характеристики управляемости:

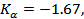
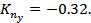
Подадим на вход системы сигнал .

Построим переходные процессы по всем координатам.

Передаточная функция по углу атаки:

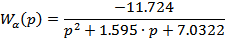
Рис. 2. П/п по углу атаки .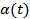

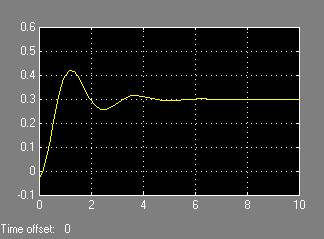
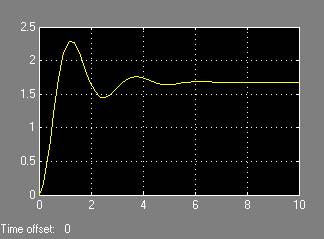
Передаточная функция по нормальной перегрузке:

Рис. 3. П/п по нормальной перегрузке .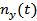

Передаточная функция по углу наклона траектории:

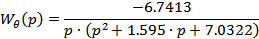
Рис. 4. П/п по углу наклона траектории

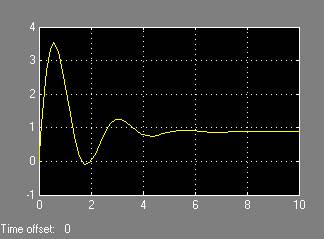
Передаточная функция по угловой скорости:

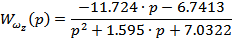
Рис. 5. П/п по угловой скорости .

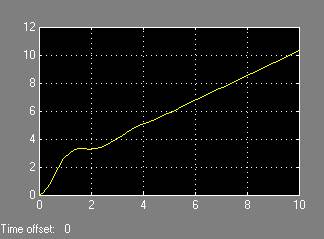
Передаточная функция по углу тангажа:

Рис. 6. П/п по углу тангажа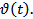

Передаточная функция по высоте:

Рис. 7. П/п по высоте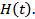

Выводы по п.1 работы: ДИНАМИКА САМОЛЁТА.

По дифференциальным уравнениям продольного движения была построена структурная схема в рабочей среде Simulink. Были выведены передаточные функции по основным координатам и проанализированы статические и динамические характеристики самолёта. По построенным графикам был проведен анализ и сравнение с расчётными данными. Параметры построенных графиков имеют незначительные отклонения от расчётных в связи с тем, что при расчётах был принят равным нулю динамический коэффициент .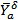

2. ДИНАМИКА САМОЛЁТА С УЧЁТОМ ДИНАМИКИ ПРИВОДА.

В первой части работы динамика самолёта изучалась при условии, что передаточная функция привода представляет собой пропорциональное звено с коэффициентом передачи равным 1. В реальности, привод не является линейным. Изучим динамику привода при управлении самолётом в продольном канале на основе модели, приведенной на рисунке 8.

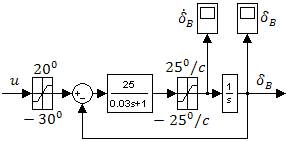
Рис. 8. Структурная схема привода рулей высоты.

Подадим на вход системы сигнал .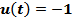

Построим переходные процессы по углу атаки, скорости привода и его перемещению.

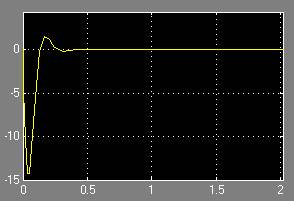
Рис. 9. П/п по скорости привода

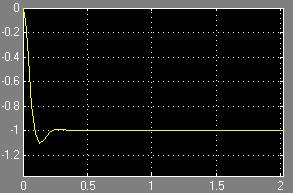
Рис. 10. П/п по перемещению привода

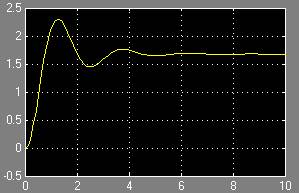
Рис. 11. П/п по углу атаки .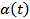

Сравнивая переходные процессы по углу атаки в п.1 работы (рис. 2) и с учётом привода (рис. 11), можно сделать вывод, что динамика привода при малых входных воздействиях практически не влияет на динамику самолёта.

Подадим на вход системы сигнал .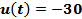

Построим переходные процессы по углу атаки, скорости привода и его перемещению.

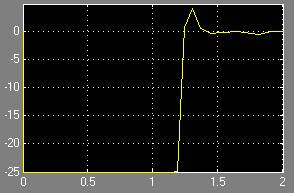
Рис. 12. П/п по скорости привода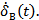

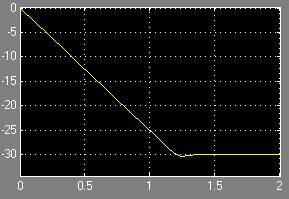
Рис. 13. П/п по перемещению привода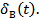

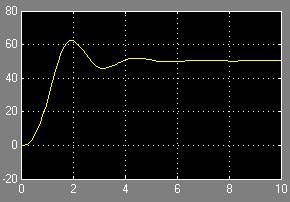
Рис. 14. П/п по углу атаки .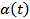

Сравнивая переходные процессы по углу атаки при больших и малых входных воздействиях, можно сделать вывод, что динамика привода оказывает существенное воздействие на быстродействие самолёта при больших входных воздействиях.

Выводы по п.2 работы: ДИНАМИКА САМОЛЁТА С УЧЁТОМ ДИНАМИКИ ПРИВОДА.

Во втором пункте работы в структурную схему самолёта была добавлена схема привода. Его динамика была изучена при малых и больших входных воздействиях.

При малом входном сигнале (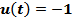) привод занимает заданное положение всего за 0.2 секунды.

При большом входном сигнале (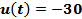) привод занимает заданное положение за 1.2 секунды.

Эта разница во времени обусловлена ограничением привода по скорости. Следовательно, чем сильнее нужно отклонить рули высоты, тем большее время для этого понадобится. Эта особенность реальных приводов существенно влияет на время переходных процессов самолёта.

Дата добавления: 2015-10-21