Алгоритм вычисления медианы статистического ряда

Условие: длина каждого интервала статистического ряда равна .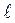

1. Прежде всего, определяется так называемый медианный интервал. Для этого вычисляется число 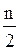, равное половине всего количества выборочных значений. Затем последовательно складываются частоты первого, второго и так далее интервалов до тех пор, пока не получится сумма, которая либо равна 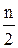, либо чуть больше 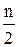. Интервал, соответствующий последней прибавленной частоте, и будет являться медианным. Допустим, что сумма частот первых s интервалов не меньше числа 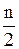, то есть

,

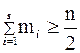но сумма частот нижних s – 1 интервалов меньше 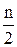, то есть

.

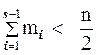Тогда именно s -й интервал 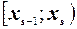является медианным.

2. Далее медиана статистического ряда вычисляется по формуле:

Х .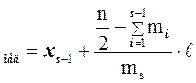

Подчеркнем, что 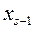– это нижняя граница медианного интервала, n – объем всей выборки, 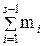– сумма частот всех интервалов, расположенных ниже медианного, – частота медианного интервала, 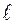– длина каждого интервала.

Пример 2.5 Найдем медиану статистического ряда по данным о возрасте пациентов поликлиники.

Таблица 2.5 – Данные исследования о возрасте пациентов поликлиники

Возраст	10–20	20–30	30–40	40–50	50–60	60–70	70–80	80–90

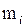
Объем всей выборки n = 250, поэтому 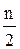= 125. Последовательно складываем частоты пока не получим сумму, равную или большую 125:

17 + 24 + 35 + 48 = 124, но

17 + 24 + 35 + 48 + 57 = 181.

Сумма частот первых четырех интервалов меньше 125, а сумма частот пяти интервалов больше 125, поэтому именно пятый интервал [50; 60) является медианным. Вычислим медиану по данной формуле:

Х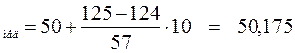

или

Х .

Это значение медианы показывает, что возраст половины пациентов в данной выборке не больше 50 лет и 2 месяцев.

■

Пример 2.6 Найдем медиану статистического ряда из примера 1.8, представляющего данные о высоте зданий.

Таблица 2.6 – Статистический ряд измерений высоты зданий

Высота зданий	5–10	10–15	15–20	20–25	25–30	30–35	35–40	40–45	45–50

Объем всей выборки 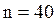, поэтому 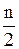= 20. Находим последовательно суммы частот:

2 + 3 + 5 + 6 = 16 < 20,

но 2 + 3 + 5 + 6 + 8 = 24 > 20.

Поэтому пятый интервал [25; 30) является медианным.

Вычислим медиану по указанной выше формуле:

Х .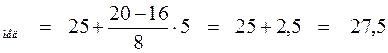

Следовательно, X _мед = 27,5. Это значение показывает, что в исследуемой выборке половина зданий имеет высоту не более 27,5 метров.

■

Заметим, что медиана существует в любой статистической выборке. Следует подчеркнуть и такое полезное свойство медианы как её нечувствительность к месторасположению экстремальных значений в больших выборках. Наличие в выборке сильно отклоняющихся значений создает определенные проблемы при анализе, поэтому использование медианы позволяет в определенных случаях обойти некоторые трудности.

Известно, что существуют симметричные и асимметричные распределения случайных величин. В том случае, когда выборочные данные реализуют симметричное распределение, то значение медианы и моды практически совпадают. Для асимметричных распределений равенство не выполняется.

Дата добавления: 2015-10-21