Полученные результаты заносятся в таблицу представляющую статистический ряд.

Пример 1.8 Составим статистический ряд по данным измерений высот 40 зданий города.

7,2	15,2	20,8	24,6	27,5	30,6	34,7	38,5
9,6	16,3	22,4	25,1	28,3	31,8	35,6	42,3
10,5	17,2	23,5	25,7	28,8	32,3	35,8	43,4
12,8	18,4	23,7	26,4	29,4	33,2	36,2	44,5
14,2	18,8	24,5	27,2	30,4	34,5	37,4	48,5

Будем строить статистический ряд для девяти интервалов: k = 9, n = 40.

Наименьшее выборочное значение равно 7,2, наибольшее – 48,5. Определим длину каждого интервала. Найдем

= .

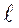Округлив полученное число до ближайшего целого, будем считать, что длина интервала 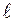= 5.

В качестве нижней границы всех наблюдаемых значений выберем число 5. Тогда имеем следующие интервалы:

[5;10), [10;15), [15;20), [20;25), [25;30), [30;35), [35;40), [40;45), [45;50].

Теперь считаем частоту выборочных значений для каждого интервала:

; ; ; ; ; ; ; ; .

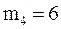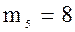Проверка подтверждает правильность равенства

.

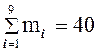Далее вычисляем относительные частоты:

; ; ; ;

; ; ; ; .

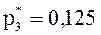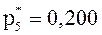Суммирование относительных частот показывает, что равенство выполняется. Запишем статистический ряд.

Таблица 1.7 – Статистический ряд измерений высоты зданий

Высота зданий	5–10	10–15	15–20	20–25	25–30	30–35	35–40	40–45	45–50
	0,050	0,075	0,125	0,150	0,200	0,175	0,125	0,075	0,025

■

Вместо короткого названия статистический ряд часто используются более точные по смыслу такие названия, как статистическое распределение выборки, или статистический закон распределения.

Напомним, что в теории вероятностей законом распределения дискретной случайной величины называется соответствие между всеми её возможными значениями и их вероятностями. Статистическое распределение отличается от теоретического вероятностного распределения тем, что вероятность отдельных значений в математической статистике заменяется их относительной частотой.

Дата добавления: 2015-10-21