Читайте также:
|
1. Положим r = 0.
2. Положим r = r +1.
3. Проверяем условие
≥ 
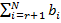. (7)
Если (7) выполняется, то сделаем следующее.
3.1. Положим
xr = (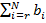
– 
) ⁄ (ar + br). (8)
3.2. Положим xi = 1 (i = 1, …, r –1), xi = 0 (i = r +1, …, N).
3.3. Стоп. Алгоритм прекращает работу.
В противном случае переходим на шаг 2.
В силу равенства (1) легко понять, что условие (7) обязательно будет выполнено при ка-ком-либо r. Нетрудно проверить, что xr, определяемое формулой (8), лежит между 0 и 1. Более сложным является центральное в данном разделе
Утверждение 2. Делёж, построенный описанным выше алгоритмом ПП, является спра-ведливым для любых сравнительных важностей a 1, …, aN и b 1, …, bN. Единственный пункт, который может делиться в построенном платеже – это r -ый пункт, где r – минимальный индекс, удовлетворяющий условию (7) ■
Пример 5. Рассмотрим задачу дележа, данные которой представлены в таблице 1. После
Таблица 1
| Таблица 2
|
перенумерации пунктов в соответствии с формулой (6) получим задачу, представленную в таб-лице 2 (в 1-м столбце в скобках указаны исходные номера пунктов).
Далее последовательно проверяем, начиная с r = 1, условия (7), используя нумерацию пунктов из таблицы 2. При r = 1 имеем
= a 1 = 27, 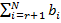= b 2 + b 3 + b 4 + b 5 = 12 + 29 + 21 + 28 = 90. Так как 27 < 90, то условие (7) не выполняется.
Далее, при r = 2,
= a 1 + a 2 = 27 + 26 = 53, 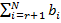= b 3 + b 4 + b 5 = 29 + 21 + 28 = 78. Так как 53 < 78, то условие (7) не выполняется.
Далее, при r = 3,
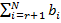= a 1 + a 2 + a 3 = 27 + 26 + 23= 76, = b 4 + b 5 = 21 + 28 = 49. Так как 76 ≥ 49, то условие (7) выполняется. Поэтому, в соответствии с операциями на шаге 3, получаем
xr = (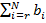 – ) ⁄ (ar + br) = (78 – 53) ⁄ (23 + 29) = 25 ⁄ 52 = 0,48.
Таким образом, построенный делёж таков: x = (1; 1; 0,48; 0; 0). Это означает, что 1-ый и 2-ой пункты целиком достаются участнику A, 4-ый и 5-ый пункты – участнику B; 3-ий пункт делится между ними в пропорции 0,48:0,52. Переходя к исходной нумерации пунктов, приве-дённой в левом столбце таблицы 2, окончательно получаем следующее. Участник A целиком получает 1-ый и 3-ий пункты, участник B – 2-ой и 4-ый пункты, а 5-ый пункт делится между участниками в той же пропорции 0,48:0,52. Поэтому окончательный делёж принимает вид: x = (1; 0; 1; 0; 0,48).
Зная делёж x, можно по формулам (2) подсчитать выигрыши участников. Имеем
G A(x) = 
= 26•1+11•0+27•1+13•0+23•0,48 ≈ 64,06;
G B(x) = 
) = 12•0+28•1+10•0+21•1+29•0,52 ≈ 64,06.
Примерное равенство выигрышей здесь не случайное совпадение, а следствие утверждения 2. Если считать не в десятичных, а в простых дробях, получится точное равенство. Поскольку по-строенный делёж является справедливым, то оба участника получают одинаковую сумму бал-лов просто по определению справедливого дележа. Из формулы (5) ясно также, что построен-ный делёж свободен от зависти. В силу того же утверждения 2 делёж x Парето-эффективен ■
Пример 6. Рассмотрим задачу дележа, данные которой представлены в таблице 3. После
Таблица 3
| Таблица 4
|
перенумерации пунктов в соответствии с формулой (6) получим задачу, представленную в таб-лице 4 (в 1-м столбце в скобках указаны исходные номера пунктов). Далее последовательно проверяем, начиная с r = 1, условия (7), используя нумерацию пунктов из таблицы 4. При r = 1 имеем = a 1 = 90, 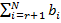= b 2 + b 3 + b 4 + b 5 = 20 + 20 + 20 + 20 = 80. Так как 90 ≥ 80, то условие (7) выполняется. Поэтому, в соответствии с операциями на шаге 3, получаем
x 1 = (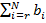 – ) ⁄ (ar + br) = (100 – 0) ⁄ (90 + 20) = 100 ⁄ 110 = 10 ⁄ 11; x 2 = x 3 = x 4 = x 5 = 0.
Возвращаясь к исходной нумерации пунктов, приведённой в левом столбце таблицы 4, окончательно получаем следующее. Участник A получает только 10 ⁄ 11 4-го пункта, участник B – 1 ⁄ 11 4-го пункта и все остальные пункты целиком. Поэтому окончательный делёж прини-мает вид: x = (0; 0; 0; 0,91; 0). Зная делёж x, можно по формулам (2) подсчитать выигрыши учас-тников. Имеем
G A(x) = = 2•0+ 3•0+ 2•0+90•(10 ⁄ 11)+3•0 = 81 
;
G B(x) = ) = 20•1+20•1+20•1+20•(1 ⁄ 11)+20•1 =.81 ,
Как и в примере 5, легко проверить, что данный делёж является справедливым. Заметим, что выигрыш обоих участников значителен. Это происходит из-за большого различия в оценках ■
Задание 2. Найти справедливые дележи и соответствующие им выигрыши алгоритмом ПП. В качестве образца использовать примеры 5 и 6.
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
■
2.3. Неделимые пункты. Задача справедливого дележа часто возникает при слиянии двух компаний (см. [3]). Речь идёт не столько о финансовых проблемах (которые обычно разрешают-ся в соответствии с имеющимися у компаний акциями и другими активами), сколько о так на-зываемых «социальных» вопросах: как власть, должности и местопребывание делятся между менеджерами сливающихся компаний. Во многих случаях эти вопросы таковы:
название объединённой компании;
местопребывание штаб-квартиры;
назначение на должности президента и генерального директора;
сокращение служащих с целью избежать дублирования операций после слияния.
Пример 7. Важности, которые каждая из двух сливающихся фирм A и B придаёт указан-ным выше пунктам, приведены в таблице 5. Заметим, что речь идёт именно о важности, а не о положительном или отрицательном отношении к данному пункту. Например, если по пункту сокращений фирмы указывают 5% и 15%, то это значит, что сокращение 3Х сотрудников 1-ой фирмой равносильно сокращению Х сотрудников 2-ой фирмой (для неё это более значимый вопрос). Конечно, назначение на должности президента и гендиректора имеет для обеих фирм положительное значение. В таблице 6 приведены те же данные в порядке, предписанном алго-ритмом ПП.
Таблица 5
| Таблица 6
|
Воспользуемся алгоритмом ПП. Проводя вычисления аналогично вычислениям в приме-рах 4 и 5, получим делёж x = (0; 0; 
; 1; 1). Это значит, что фирма A назначает директора и не проводит сокращения, фирма B определяет название и выбирает место для штаб-квартиры. Наконец, назначение на должность президента делится между фирмами в пропорции 5: 2. Вы-игрыши обеих фирм равны при этом 65 ■
Однако указанный в примере 6 делёж, хотя и является формально справедливым, вряд ли реализуем. Действительно, трудно представить должность президента (как и большинство дру-гих должностей) разделённой в некоторой пропорции (например, представитель одной фирмы является президентом в течение 5 лет, а другой – в течение 2 лет). Суть дела в том, что не толь-ко в данной ситуации, но и во многих других некоторые (а иногда и все) пункты неделимы. По-этому метод ПП может оказаться неприменимым – как раз тогда, когда неделимым оказывается тот единственный пункт, который должен делится в соответствии с методом ПП. Более того, справедливого (в указанном выше смысле) дележа может не существовать. Предположим, что в примере 6 неделимым является только 4-ый пункт (тот, который оценивается участником А в 90%). Действительно, если этот пункт достаётся целиком участнику А, то при любом дележе других пунктов его выигрыш не меньше 90, а выигрыш участника В не превосходит 80. Если же этот пункт достаётся участнику В, то его выигрыш то при любом дележе других пунктов не меньше 20, а выигрыш участника А не превосходит 10. Таким образом, в этой ситуации равно-ценность и, следовательно, справедливость дележа не может быть обеспечена.
В общем случае, т.е. при любом распределении делимых и неделимых пунктов, необходи-мые и достаточные условия существования справедливого дележа (в терминах значений важ-ности a 1, …, aN и b 1, …, bN всех пунктов) найдены сравнительно недавно (см. литературу в конце части) и здесь не приводятся. Ниже рассматривается случай 5-и пунктов, из которых только один делим, а остальные 4 неделимы. Именно такая ситуация имеет место в примере 7. В следующем примере приводится простой алгоритм, позволяющий найти справедливый де-лёж, если он есть, или установить его отсутствие.
Пример 8. Рассмотрим задачу справедливого дележа при данных в таблице 7 оценках важности пяти пунктов участниками А и B, из которых только выделенный жирным 2-ой пункт является делимым.
Таблица 7
| пп | A | B |
Поскольку 4 пункта (1-й, 3-ий, 4-ый и 5-ый) являются неделимыми, каждый из них целиком до-стаётся одному из участников. Поэтому распределение неделимых пунктов можно задать дво-ичным вектором s = (s 1, s 3, s 4, s 5), где
(i = 1, 3, 4, 5)
Выигрыши участников от неделимых пунктов при распределении s = (s 1, s 3, s 4, s 5) даются формулами
VA = 30 s 1+16 s 3+25 s 4 +17 s 5,
VB = 11(1– s 1)+22(1– s 3)+20(1– s 4)+19(1– s 5).
1. Вычислим выигрыши участников только от неделимых пунктов при всех распределени-ях s = (s 1, s 3, s 4, s 5) (их всего 16) и запишем их в следующую таблицу.
|
|
При добавлении какой-либо части 2-го пункта к выигрышу V A он не может увеличиться боль-ше, чем на 12. Аналогично, выигрыш V B не может увеличиться больше, чем на 28. Поэтому все строчки таблицы, в которой V B – V A > 12 и все строчки таблицы, в которой V A – V B > 28, не соответствуют справедливому дележу (в них разница между выигрышами участников не может быть компенсирована за счёт деления одного делимого 2-го пункта). Поставим в самом правом столбце таблицы знак «–» во всех таких строчках. Если все 16 строчек таблицы содержат мину-сы, то это означает отсутствие справедливого дележа при данных условиях.
2. Рассмотрим теперь все строчки таблицы, в правой позиции которых нет минусов. Слева от правого столбца стоит пара чисел – выигрыши V A и V B при соответствующем распределении неделимых пунктов. В данном случае эти пары таковы: (42,43), (33,31), (41,30), (47,42), (55,41), (46,39). Сравним, например, пару (47,42) с парой (46,39). Если распределение неделимых пунктов даёт выигрыши 47 и 42 (см. таблицу выше), то при любом делении 2-го пункта оба участника получают больше, чем при том же самом делении 2-го пункта и распределении неделимых пунктов, дающих выигрыши 46 и 39. Это рассуждение показывает, что все домини-руемые по Парето пары можно далее не рассматривать. Поставим знак * в строчки, соответст-вующие таким доминируемым парам выигрышей. В результате останутся ничем не помеченные строчки, содержащие недоминируемые по Парето пары (47,42) и (55,41).
3. Каждую из оставшихся пар надо проанализировать следующим образом.
3.1. Пара (47,42) соответствует дележу, при котором участник A получает пункты 1 и 5 (в сумме 47 баллов), а участник B – пункты 3 и 4 (в сумме 42 балла). Осталось разделить делимый 2-ой пункт. Пусть x – доля 2-го пункта, получаемая участником A. Из условия равенства баллов имеем
47 + 12 x = 42 + 28(1– x).
Решая уравнение, находим x = 23 ⁄ 40 = 0,575; далее 47 + 12*0,575 = 53,9 и каждый участник получает по 53,9 балла.
3.2. Пара (55,41) соответствует дележу, при котором участник A получает пункты 1 и 4 (в сумме 55 баллов), а участник B – пункты 3 и 5 (в сумме 41 балл). Из условия равенства баллов имеем
55 + 12 x = 41 + 28(1– x).
Решая уравнение, находим x =14 ⁄ 40 =0,35; далее 55+12*0,35=59,2 и каждый участник получает по 59,2 балла. Поскольку во 2-м случае выигрыш участников больше, то это решение и соответ-ствует справедливому дележу. В данном случае справедливый делёж x = (1; 0,35; 0; 1; 0).
Если же неотмеченным в таблице оказывается только один вариант, то он и есть опти-мальный. Но и в этом случае надо решить аналогичное уравнение и чётко указать, кто что полу-чает и чему равен выигрыш участников (напомним, что по определению справедливого дележа выигрыши участников должны совпадать) ■
Пример 9. Продолжение примера 7. Рассмотрим задачу справедливого дележа при дан-ных в таблице 5 оценках важности пяти пунктов участниками А и B. Эти же данные приведены в таблице 8 без названий пунктов. Последняя строчка, соответствующая единственному дели-мому пункту – сокращениям – выделена жирным.
Таблица 8
| Пункт | A | B |
| Всего |
Применим метод, подробно описанный в примере 8. Выигрыши участников от неделимых пунктов при распределении s = (s 1, s 2, s 3, s 4) даются формулами
VA = 10 s 1+20 s 2+15 s 3 +25 s 4,
VB = 25(1– s 1)+35(1– s 2)+20(1– s 3)+10(1– s 4).
1. Вычислим выигрыши участников только от неделимых пунктов при всех распределени-ях s = (s 1, s 2, s 3, s 4) (их всего 16) и запишем их в следующую таблицу.
|
|
При добавлении какой-либо части 5-го пункта к выигрышу V A он не может увеличиться боль-ше, чем на 30. Аналогично, выигрыш V B не может увеличиться больше, чем на 10. Поэтому все строчки таблицы, в которой V B – V A > 30 и все строчки таблицы, в которой V A – V B > 10, не соответствуют справедливому дележу (в них разница между выигрышами участников не может быть компенсирована за счёт деления одного делимого 5-го пункта). Поставим в самом правом столбце таблицы знак «–» во всех таких строчках..
2. Рассмотрим теперь все строчки таблицы, в правой позиции которых нет минусов. В данном случае эти пары таковы: (40,60), (45,45), (35,35), (35,55), (25,45), (30,30). Из этих 6-и пар недоминирумыми по Парето будут пары (40,60) и (45,45). Все остальные пары доминируемы хотя бы одной из этих двух.
3.1. Пара (40,60) соответствует дележу, при котором участник A получает пункты 3 и 4 (в сумме 40 баллов), а участник B – пункты 1 и 2 (в сумме 60 баллов). Осталось разделить дели-мый 5-ой пункт. Пусть x – доля 5-го пункта, получаемая участником A. Из условия равенства баллов имеем
40 + 30 x = 60 + 10(1– x).
Решая уравнение, находим x = 0,75; далее 40 + 12*0,75 = 62,5 и каждый участник получает по 62,5 балла.
3.2. Пара (45,45) соответствует дележу, при котором участник A получает пункты 2 и 4 (в сумме 45 баллов), а участник B – пункты 1 и 3 (в сумме 45 баллов). Из условия равенства баллов имеем
45 + 30 x = 45 + 10(1– x).
Решая уравнение, находим x = 0,25; далее 45 + 30*0,25 = 52,5 и каждый участник получает по
52,5 балла.
Поскольку во 1-ом случае выигрыш участников больше, то это решение и соответствует справедливому дележу. В данном случае справедливый делёж x = (0;; 0; 1; 1; 0,75). Заметим, что выигрыш 62,5 балла меньше выигрыша 65 , получаемого методом ПП. Это неудивительно, поскольку решение, в отличие от метода ПП, теперь ищется не на множестве всех дележей, а на вложенном в него множестве дележей, удовлетворяющих дополнительным условиям на деле-ние пунктов 1 – 4 ■
Задание 3. Найти справедливые дележи и соответствующие им выигрыши для данных из задания 2 алгоритмом, описанным и продемонстрированным в примерах 8 и 9. Результаты зада-ний 2 и 3 с одними и теми же номерами сравнить. Единственным делимым пунктом является пункт, выделенный жирным шрифтом ■
Пример 10. Рассмотрим задачу дележа с исходными данными, приведёнными в таблице 9:
Таблица 9
| Пункт | A | B |
| Всего |
В данном случае предполагается, что пункты 1 и 2 делимы, а пункты 3, 4 и 5 – неделимы. Рас-смотрим следующие два дележа: x = (0; 2⁄3; 1; 0; 1), y = (0; 0; 1; 1; 0). При дележе x участник A получает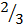 
пункта 2 и пункты 3 и 5 целиком; участник B – 
пункта 2 и пункты 1 и 4 цели-ком; оба выигрыша равны 56 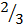. При дележе y участник A получает пункты 3 и 4 целиком, участник В – пункты 1, 2 и 5 целиком; выигрыш участника A равен 65, а выигрыш участника В – 62. Оба дележа свободны от зависти, однако делёж x не является Парето-эффективным (при дележе y оба участника получают больше), а делёж y не является равноценным. Поэтому оба дележа не являются справедливыми в смысле введённого определения.
Можно убедиться, что в данном случае справедливого дележа просто не существует. Воп-рос о том, какой из двух рассмотренных дележей является «более» справедливым, не решается в рамках математики. Как и в других подобных случаях, суть дела в содержательных аспектах конкретной ситуации ■
Дата добавления: 2015-10-16; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Справедливый делёж | | | Пропорциональное представительство |