
Читайте также:
|
5.1. Игра размерности 2´2. Рассмотрим произвольную матричную игру со следующей платёжной матрицей размерности 2´2 общего вида:
Q =  . (18)
. (18)
Для поиска решений в смешанных стратегиях в данной игре рассматриваются два взаимоиск-лючающих случая.
Случай 1. У игры есть решение в чистых стратегиях. Тогда в силу утверждения 7 это же самое решение (представленное в виде пары смешанных стратегий, как в примере 6) является решением игры в смешанных стратегиях. На этом поиск решений в смешанных стратегиях за-кончен.
Прежде чем перейти к случаю 2 - отсутствию решения в чистых стратегиях - сформули-руем некоторые простые, но нужные для дальнейшего утверждения.
Утверждение 8. Пусть в матрице (18) есть доминируемые или дублирующие строки или столбцы. Тогда в матричной игре с этой платёжной матрицей есть решение в чистых стратегиях ■
Заметим, что условие утверждения 8 является достаточным, но не необходимым. В игре с матрицей Q =  есть решение в чистых стратегиях, а доминируемых или дублирующих строк и столбцов нет.
есть решение в чистых стратегиях, а доминируемых или дублирующих строк и столбцов нет.
Утверждение 9. Пусть в матрице (18) совпадают элементы одного столбца или одной строки. Тогда в матричной игре с этой платёжной матрицей есть решение в чистых стратегиях ■
Напомним определение функции sgn(x):
sgn(x) = 
Утверждение 10. Пусть в матрице (18)
sgn(q 11 - q 21) = - sgn(q 22 - q 12) (19a)
или
sgn(q 11 - q 12) = - sgn(q 22 - q 21). (19b)
Тогда в матричной игре с этой платёжной матрицей есть решение в чистых стратегиях ■
Случай 2. У игры нет решения в чистых стратегиях. Рассмотрим выражение (9) для выиг-рыша игрока А в игре размерности 2´2:
g (x, y) = x 1· y 1· q 11 + x 1· y 2· q 12 + x 2· y 1· q 21 + x 2· y 2· q 22. (20)
Учитывая, что x 1 + x2 = 1, y 1 + y2 = 1, положим x = x 1, y = y 1 и отождествим стратегии игроков с однозначно определяющими их вероятностями x и y. Представим (20) (после простых преобра-зований) в следующем виде:
g (x, y) = mx + n, (21a)
где
m = (q 11– q 12– q 21+ q 22)· y +(q 12 – q 22), (22a)
n = (q 21– q 22)· y + q 22. (23a)
Выражение (20) является, в соответствии с определениями, проигрышем игрока В в той же са-мой игре. Представим (20) в виде, аналогичном (21a):
g (x, y) = sy + t, (21b)
где
s = (q 11– q 12– q 21+ q 22)· x +(q 21 – q 22), (22b)
t = (q 12– q 22)· x + q 22. (23b)
Положим
q 1 = q 11 – q 12 – q 21 + q 22, (24)
q 2 = q 22– q 12, (25)
q 3 = q 22– q 21. (26)
Имеет место
Утверждение 11. Пусть в игре с платёжной матрицей (18) нет решений в чистых страте-гиях. Тогда
1) q 1 ≠ 0, q 2 ≠ 0, q 3 ≠ 0; (27)
2) sgn(q 2) = sgn(q 3); (28)
3) 0 < q 2 ¤ q 1 < 1, 0 < q 3 ¤ q 1 < 1 ■ (29)
Все три части утверждения 11 являются следствиями утверждений 8 – 10. В частности, вторые неравенства в формулах (29) следуют из того, что q 1 = q 11 – q 21+ q 2 = q 11 – q 12 + q 3 и утверждения 10.
Перейдём к явному построению решения игры в смешанных стратегиях. Начнём с игрока А. Для любой стратегии y игрока В положим
j А(y) = { x | (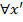 ) (g A(x', y) ≤ g A(x, y))}. (30a)
) (g A(x', y) ≤ g A(x, y))}. (30a)
Другими сдовами, j A(y) – это множество всех стратегий x игрока А, которые максимизирует его выигрыш g A(x, y) при данном y.
Положим
Φ A = {(x, y) | y Î[0, 1], x Î j A(y)}. (31a)
Множество Φ A назовём графиком игрока А (см. общее определение графика в гл. 1.3)
Поскольку при любом фиксированном y функция (21а) линейна по x, и при этом 0 ≤ x ≤ 1, то максимум достигается при m ≠ 0 на концах отрезка [0, 1] (т.е. при одной из двух чистых страте-гий), а при m = 0 – при всех стратегиях, поскольку в этом случае g (x, y) просто не зависит от x. Представим эти рассуждения геометрически, нарисовав график Φ A игрока А. Из (22а) и (23а) следует, что
g (x, 0) = – x · q 2 + q 22.
Поэтому
j (0) = 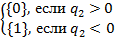 . (32a)
. (32a)
Далее, представим (22а) с учётом обозначений (24) – (26) как
m = q 1· y – q 2.
Будем увеличивать y от 0 до 1. В силу 3-ей части утверждения 11 q 1 и q 2 имеют одинаковые знаки. Поэтому при y = y * = q 2 ¤ q 1 число m = 0, g (x, y *) от x не зависит и, следовательно, мно-жеством j А(y *) является отрезок [0, 1]. Далее, при y > y * число m меняет знак на противопо-ложный. Поэтому, если j (0) = {0}, то j (1) = {1}; если же j (0) = {1}, то j (1) = {0}. Оба случая (при 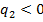 и при
и при  ) представлены на рис.1.
) представлены на рис.1.

Рис.1
Теперь перейдём к игроку В. Для любой стратегии x игрока А положим
y B(x) = { y | ( ) (g B(x, y) ≤ g B(x, y
) (g B(x, y) ≤ g B(x, y  ))}. (30b)
))}. (30b)
Другими сдовами, y B(x) – это множество всех стратегий y игрока B, которые минимизируют его выигрыш g B(x, y) при данном x.
Определим график игрока В формулой, аналогичной формуле (31а):
Y В = {(x, y) | x Î[0, 1], y Î y B(x)}. (31b)
Далее практически повторим все рассуждения относительно графика Φ A применительно к гра-фику Y В (учитывая минимизацию, а не максимизацию). В частности, получим
y (0) =  (32b)
(32b)
(различие (32a) и (32b) определяется минимизацией вместо максимизации).
Как и выше, положим x * = q 3 ¤ q 1. При x = x * коэффициент s при y в (21b) обращается в 0, так что минимум достигается при любом y от 0 до 1; в этой точке знак s меняется и, соответствен-но, y (x) меняет значение с {0} на {1} или наоборот. Оба случая представлены на рис.2 в тех же координатах, что и на рис.1.
В силу формулы (28), q 2 < 0 тогда и только тогда, когда q 3 < 0. Поэтому при изображении обоих графиков в одних и тех же координатах имеется два случая: q 2 < 0, q 3 < 0 и q 2 > 0, q 3 > 0. Других вариантов не может быть. Эти графики показаны на рис. 3. Из формулы (29) следует, что q 1 имеет тот же знак, что q 2 и q 3. Поэтому левой и правой части рис.3 соответствуют q 1 < 0 и q 1 > 0.
Суть дела состоит в том, что найденные смешанные стратегии x * и y * образуют решение исходной матричной игры с платёжной матрицей (18), не имеющей решений в чистых стратеги-ях. Действительно, по построению j А(y) (см. формулу (30a)) для любого y и для любого x'  j А(y) выполняется условие
j А(y) выполняется условие
( x) g (x, y) ≤ g (x', y). (33a)
x) g (x, y) ≤ g (x', y). (33a)
В частности, (33a) верно при y = y * и x' = x *, так как при y = y * x' можно выбрать произвольно. Поэтому из (33a) следует, что для любого x
g (x, y *) ≤ g (x *, y *). (34a)
Аналогично, по построению y B(x) для любого x и для любого y' = y (x) выполняется условие
(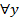 ) g (x, y') ≤ g (x, y). (33b)
) g (x, y') ≤ g (x, y). (33b)
В частности, (33b) верно при y' = y * и x = x *, так как при x = x * y' можно выбрать произвольно.
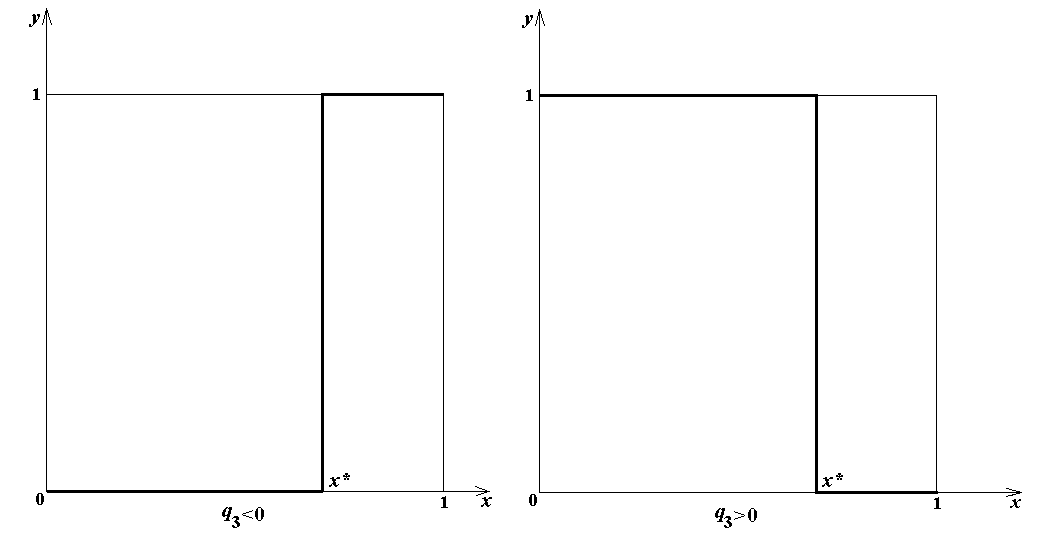
Рис.2

Рис.3
Поэтому из (33b) следует, что для любого y
g (x *, y *) ≤ g (x *, y). (34b)
Неравенства (34a) и (34b) вместе совпадают с двойным неравенством (12), т.е. пара стратегий á x *, y *ñ по определению является решением игры в смешанных стратегиях.
Если «принять на веру» утверждения 8 - 11 (доказательства которых достаточно просты), то вместе с предыдущими рассуждениями они доказывают существование решения в смешан-ных стратегиях любой игры размерности 2´2 для произвольной платёжной матрицы (18). Ко-нечно, этот факт сам по себе непосредственно следует из общего утверждения 6. Однако оно является типичной «теоремой существования», не объясняющей, как находить само решение.
Для игр размерности 2´2 ситуация другая. Числа x * и y * определены в явном виде:
x * = q 3 ¤ q 1, y * = q 2 ¤ q 1,
где числа q 1, q 2и q 3выражаются через элементы исходной платёжной матрицы (18) по форму-лам (24) - (26). Переходя обратно от задания смешанной стратегии одним числом (вероятнос-
тью выбора 1-ой стратегии) к её заданию парами чисел (см. текст после формулы (20)), оконча-
тельно получаем
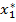 =
= 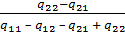 ,
,  = 1-
= 1- 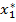 , x * = (
, x * = (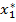 ,
,  ); (35a)
); (35a)
 =
= 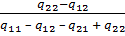 ,
,  = 1-
= 1-  , y * = (
, y * = ( ,
,  ). (35b)
). (35b)
При взгляде на формулы (35) возникает вопрос – что делать, если входящий в них делитель (24) окажется равным 0? Ведь на 0 делить нельзя! При этом число q 1, определяемое формулой (24), действительно может быть равным 0 – например, в платёжной матрице  . Однако для платёжных матриц без седловой точки (а только такие матрицы здесь и рассматри-ваются) выражение (24) не равно 0 (см. 1-ую часть утверждения 11). Так что на 0 делить не придётся.
. Однако для платёжных матриц без седловой точки (а только такие матрицы здесь и рассматри-ваются) выражение (24) не равно 0 (см. 1-ую часть утверждения 11). Так что на 0 делить не придётся.
Таким образом, полностью решена задача нахождения решения матричной игры размер-ности 2´2 для произвольной платёжной матрицы (18). Если у игры есть решение в чистых стра-тегиях, то оно и является искомым решением. В том и только том случае, если такого решения нет, можно найти решение в смешанных стратегиях по формулам (35).
Пример 7. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей: Q =  . Найдём её решение. Поскольку у данной игры нет решения в чистых стратегиях, то воспользуемся формулами (35), положив q 11 = 6, q 12 = 2, q 21 = 5, q 22 = 8. Получим
. Найдём её решение. Поскольку у данной игры нет решения в чистых стратегиях, то воспользуемся формулами (35), положив q 11 = 6, q 12 = 2, q 21 = 5, q 22 = 8. Получим
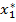 =
= 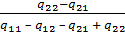 =
= 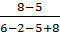 =
=  ;
;  =
= 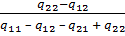 =
= 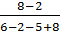 =
=  ;
;
 = 1-
= 1- 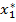 = 1 -
= 1 -  =
=  ;
;  = 1-
= 1-  = 1 -
= 1 -  =
=  ; x * = (
; x * = ( ,
,  ); y * = (
); y * = ( ,
,  ) ■
) ■
Задание 3. Найти решения в следующих матричных играх (см. пример 7)
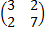
| 
| 
| 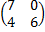
| 
| 
| 
|
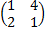
| 
| 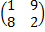
| 
| 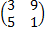
| 
| 
|

| 
| 
| 
| 
| 
| 
|

| 
| 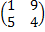
| 
| 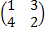
| 
| 
|
■
5.2. Игра размерности 2´ n. Рассмотрим произвольную матричную игру со следующей платёжной матрицей размерности 2´ n общего вида:
Q =  . (36)
. (36)
Оказывается, что для игр с платёжной матрицей вида (36) решение может быть найдено графо-аналитическим методом. Для простоты решение излагается для n = 4 в следующих двух примерах.
Пример 8. Найдём решение и цену игры с платёжной матрицей Q =  . Преж-де всего проверим наличие (или отсутствие) решения в чистых стратегиях. В данном случае
. Преж-де всего проверим наличие (или отсутствие) решения в чистых стратегиях. В данном случае
max i min j qij =max{2, 4} = 4; min j max i qij = min{4, 8, 6, 6} = 4.
Так как max i min j qij = min j max i qij = q 21, то пара чистых стратегий á2, 1ñ является решением дан-ной игры. Как и в примере 6, представим эти чистые стратегии как смешанные: x = (0, 1); y = (1, 0, 0, 0). Ценой игры является общее значение максимина и минимакса, равное q 21 = 4 ■
Пример 9. Найти решение и цену игры с платёжной матрицей Q =  . В этом случае та же самая проверка даёт
. В этом случае та же самая проверка даёт
max i min j qij = max{3, 4} = 4; min j max i qij = min{6, 8, 6, 6} = 6.
Поскольку в данном случае max i min j qij < min j max i qij, то решений в чистых стратегиях нет.
Поэтому можно и нужно искать решение игры в смешанных стратегиях описанным ниже гра-фо-аналитическим методом.
Игрок A имеет только 2 чистых стратегии. Его задача состоит в максимизации своего выигрыша в зависимости от своей смешанной стратегии (x 1, x 2)
v (x 1, x2) =  (q 1 j x 1 + q 2 j x 2), (37)
(q 1 j x 1 + q 2 j x 2), (37)
где минимум берётся по 4-ём чистым стратегиям игрока B.
Так как x 2 = 1 - x 1, то, обозначая x 1 через x, из (40) получаем выражение
v (x) =  {(q 1 j - q 2 j) x + q 2 j }. (38)
{(q 1 j - q 2 j) x + q 2 j }. (38)
Таким образом, v (x) является минимумом четырёх линейных функций одной переменной x; можно начертить графики этих функций и затем максимизировать их минимум v (x) графичес-ким методом.
Нетрудно построить графики функций (q 1 j - q 2 j) x + q 2 j, если заметить, что они должны проходить через точки (0, q 2 j) и (1, q 1 j). Эти графики изображены на рис.4. В данном случае имеем четыре прямых линии, нижняя огибающая которых v (x) выделена жирным. Высшая точ-ка функции v (x) находится на пересечении прямых y = 2 x + 4 и y = -3 x + 6, соответствующих 3-му и 4-му столбцам матрицы Q (напомним, что j -ая прямая по построению проходит через точ-ки (0, q 2 j) и (1, q 1 j)). Поскольку в данном случае ломаная v (x) состоит только из двух звеньев, со-единённых в точке D, то указанные два столбца находятся сразу. Если же точек, где соединяют-ся звенья ломаной, несколько, то надо взять ту из них, у которой ордината максимальна. Имен-но нахождение такой точки и делается графически. Большой точности в построениях не требу-ется, поскольку всё, что нужно – это найти те два столбца, которые соответствуют двум лини-ям, определяющим эту точку.
Далее для вычисления оптимальных смешанных стратегии надо рассмотреть 2×2 матрицу P, образованную найденными выше двумя столбцами. В данном случае это 3-ий и 4-ый столб-цы, а сама матрица имеет вид:
P = 
(см. исходную матрицу Q). Для этой матрицы найдём решение в смешанных стратегиях спосо-бом, подробно описанном в примере 7. Имеем в данном случае q 11= 6, q 12= 3, q 21= 4, q 22= 6. Поэтому в силу формул (35)

Рис.4
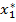 =
= 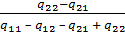 =
= 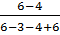 = 0,4;
= 0,4;  =
= 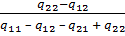 =
=  = 0,6;
= 0,6;
 = 1-
= 1- 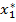 = 1 - 0,4 = 0,6;
= 1 - 0,4 = 0,6;  = 1-
= 1-  = 1 - 0,6 = 0,4.
= 1 - 0,6 = 0,4.
Теперь вспоминаем, что в исходной матрице размера 2×4 у игрока A есть две чистых стратегии: выбор 1-й или 2-й строки. В данном случае имеем
x * = (0,4; 0,6).
У игрока B есть четыре чистых стратегии, соответствующие выбору одного из 4-ёх столбцов за-данной матрицы. Однако активными (т.е. отличными от 0) являются только те две стратегии, которые соответствуют выбранным (с помощью рисунка) столбцам. В нашем случае это столб-цы 3 и 4. Вероятность выбора 3-его и 4-го столбца была найдена выше: 0,6 и 0,4. Сама опти-мальная стратегия игрока B имеет вид
y * = (0; 0; 0,6; 0,4).
Цена игры V с исходной матрицей Q совпадает с ценой игры с матрицей P. В силу 3-ьей части утверждения 5 и формулы (9) получаем
V = 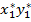 ·6 +
·6 +  ·3 +
·3 +  ·4 +
·4 +  ·6 = 0,4·0,6·6 + 0,4·0,4·3 + 0,6·0,6·4 + 0,6·0,4·6 = 1,44 + 0,48 + 1,44 + 1,44 = 4,8 ■
·6 = 0,4·0,6·6 + 0,4·0,4·3 + 0,6·0,6·4 + 0,6·0,4·6 = 1,44 + 0,48 + 1,44 + 1,44 = 4,8 ■
Задание 4. Найти решение и цену в игре со следующей платёжной матрицей (см. примеры 8 и 9).
 01 01
|  02 02
| 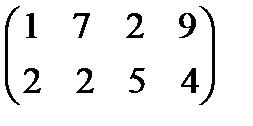 03 03
|  04 04
| 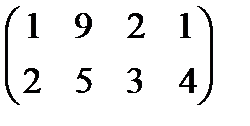 05 05
|
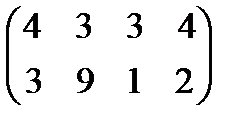 06 06
|  07 07
|  08 08
|  09 09
|  10 10
|
 11 11
| 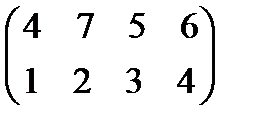 12 12
|  13 13
|  14 14
| 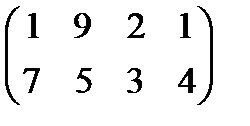 15 15
|
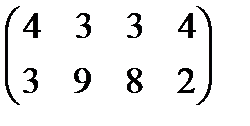 16 16
| 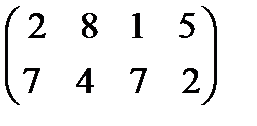 17 17
|  18 18
|  19 19
|  20 20
|
 21 21
|  22 22
|  23 23
|  24 24
| 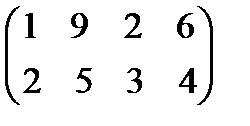 25 25
|
 26 26
| 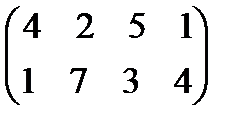 27 27
| 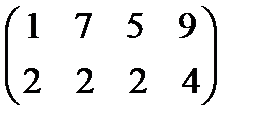 28 28
|  29 29
|  30 30
|
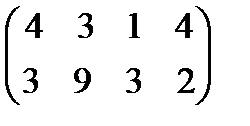 31 31
|  32 32
|  33 33
|  34 34
|  35 35
|
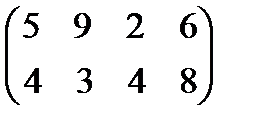 36 36
|  37 37
|  38 38
|  39 39
| 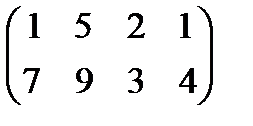 40 40
|
 41 41
| 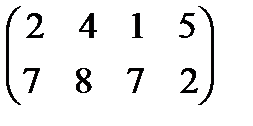 42 42
| 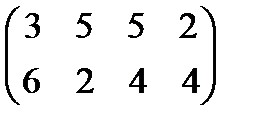 43 43
|  44 44
|  45 45
|
 46 46
| 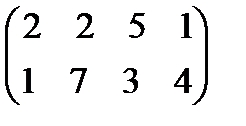 47 47
|  48 48
| 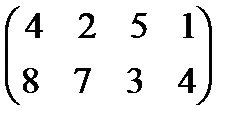 49 49
|  50 50
|
■
Во многих случаях удаётся упростить описанный выше поиск решения матричных игр с платёжной матрицей размерности 2´ n за счёт предварительного упрощения платёжной матри-цы способами, описанными в разделе 3. Проиллюстрируем это в следующем примере.
Пример 10. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей размера 2´6: Q =  . В данной матрице 1-ый, 3-ий и 4-ый столбцы домини-руемы 2-ым, 5-ым и снова 2-ым столбцами соответственно. После их удаления остаётся матри-ца P =
. В данной матрице 1-ый, 3-ий и 4-ый столбцы домини-руемы 2-ым, 5-ым и снова 2-ым столбцами соответственно. После их удаления остаётся матри-ца P =  , которая больше не упрощается. Номера её столбцов в исходной матрице та-ковы: (2, 5, 6). Далее применим описанный в примере 9 графо-аналитический метод поиска решения к матрице P. Входящие в формулу (38) три линейные функции должны проходить через точки (0, q 2 j) и (1, q 1 j) (j = 1, 2, 3). С учётом матрицы P эти точки таковы:
, которая больше не упрощается. Номера её столбцов в исходной матрице та-ковы: (2, 5, 6). Далее применим описанный в примере 9 графо-аналитический метод поиска решения к матрице P. Входящие в формулу (38) три линейные функции должны проходить через точки (0, q 2 j) и (1, q 1 j) (j = 1, 2, 3). С учётом матрицы P эти точки таковы:
(0, 2) и (1, 5); (0, 4) и (1, 1); (0, 3) и (1, 3).
Изобразим соответствующие отрезки на рис.5. Функция v (x), определённая формулой (38), пока-зана жирной линией. Эта линия состоит из двух отрезков, пересекающихся в точке D. Сами от-резки соответствуют 1-му и 2-му столбцам матрицы P. Матрица R, образованная этими столбца-ми, такова: R = 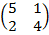 . Аналогично тому, как это делалось в примере 9, находим
. Аналогично тому, как это делалось в примере 9, находим
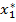 =
= 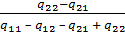 =
=  = 0,33;
= 0,33;  =
= 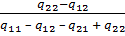 =
= 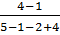 = 0,5;
= 0,5;
 = 1-
= 1- 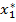 = 1 - 0,33 = 0,67;
= 1 - 0,33 = 0,67;  = 1-
= 1-  = 1 - 0,5 = 0,5.
= 1 - 0,5 = 0,5.
Поскольку рассмотренные два столбца были 2-ым и 5-ым в исходной матрице Q, получаем
x * = (0,33; 0,67) и y * = (0; 0,5; 0; 0; 0,5; 0) ■

Рис.5
Задание 5. Упростить платёжную матрицу и найти решение и цену игры в играх с матри-цами из задания 4 (см. пример 10) ■
Дата добавления: 2015-10-16; просмотров: 146 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Смешанное расширение матричных игр | | | Биматричные игры |