Решение игры

В матричной игре с платёжной матрицей Q игрок A стремится максимизировать свой выигрыш при любом выборе стратегии игроком B. Предположим, что он выбирает стратегию i Î{1,..., m }. Поскольку игрок A не знает, какую именно стратегию (т.е. какой индекс j) выбрал игрок B, то всё, что он может себе гарантировать - это выгрыш в размере

g_i = 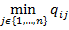. (1)

Естественно, что игрок A выберет такую стратегию i Î{1,..., m }, которая максимизирует его гарантированный выгрыш g_i. Поэтому он выбирает стратегию i *, для которой

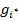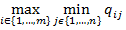= . (2)

Заметим, что при любом i Î{1,..., m } выражение 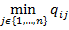, входящее в (2), не зависит от j. Поэтому значение 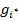зависит только от платёжной матрицы Q. Любая стратегия i *, удовлетво-ряющая условию (2), называется оптимальной стратегией игрока A (оптимальная стратегия i * может определяться неоднозначно, так как g_i может быть максимальным при различных i Î{1,..., m }).

Проведённые рассуждения показывают, что именно должен делать игрок А, чтобы до-биться максимально возможного гарантированного выигрыша. Величина 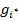, которая определя-ется только по платёжной матрице Q, называется нижней ценой игры и обозначается через V ^-.

Игрок B стремится минимизировать свой проигрыш. Предположим, что он выбирает стра-

тегию j Î{1,..., n }. Поскольку игрок B не знает, какую именно стратегию выбрал игрок А, то

всё, что он может себе гарантировать - это проигрыш в размере

f_j = 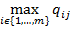. (3)

Естественно, что игрок B выберет такую стратегию j Î{1,..., n }, которая минимизирует его га-рантированный выгрыш f_j. Поэтому он выбирает стратегию j *, для которой

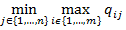= . (4)

Как и значение 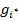, значение зависит только от платёжной матрицы Q. Любая стратегия j *, удо-влетворяющая условию (4), называется оптимальной стратегией игрока B (оптимальная страте-гия j *может определяться неоднозначно, так как f_j может быть минимальным при различных j Î{1,..., n }).

Проведённые рассуждения показывают, что именно должен делать игрок B, чтобы до-биться минимально возможного гарантированного проигрыша. Величина , которая определя-ется только по платёжной матрице Q, называется верхней ценой игры и обозначается через V ⁺.

В силу теоремы о минимаксе для любой матрицы Q имеет место неравенство

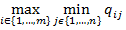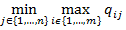≤ (5)

или, с учётом (2) и (4),

V ^- ≤ V ⁺.

Таким образом, гарантированный выигрыш игрока А не может быть больше гарантированного проигрыша игрока B.

В теории игр особенно важны те случаи, когда нижняя и верхняя цены игры совпадают. Общее значение V = V ^- = V ⁺. называется ценой игры. При этом имеет место следующее

Утверждение 1. 1) V ^-= V ⁺ тогда и только тогда, когда некоторый элемент 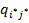платёжной матрицы Q является одновременно максимальным в её i* -ой строке и минимальным в её j* -ом столбце, т.е. для любых i Î{1,..., m } и j Î{1,..., n }

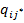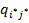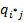≤ ≤ . (6)

2) цена игры V совпадает с 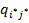; 3) стратегии i* и j* являются оптимальными ■

Пара стратегий á i*, j* ñ, удовлетворяющих требованиям утверждения 1, может определять-ся неоднозначно. Однако для всех таких пар á i*, j* ñ элементы 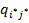платёжной матрицы Q равны одному и тому же числу - цене игры V. Всякий элемент 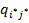платёжной матрицы Q, который является одновременно максимальным в i* -ой строке и минимальным в j* -ом столбце, называ-ется седловой точкой матрицы Q.

Заметим, что в силу неравенств (6) любому игроку оказывается невыгодным менять опти-мальную стратегию, если другой игрок будет придерживаться своей оптимальной стратегии. Для игрока А это следует из 1-го неравенства, для игрока В - из 2-го неравенства. Именно в силу разумности одновременного выбора игроками в данной ситуации своих оптимальных стратегий, любая пара стратегий á i*, j* ñ, удовлетворяющих требованиям утверждения 1, называ-ется решением игры.

Решения существуют далеко не у всех игр рассматриваемого типа. Как выбирать страте-гии в случае отсутствия седловых точек у платёжной матрицы, будет показано в разделе 4 дан-ной главы.

Пример 1. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:

Q = . (7)

Найдём, в соответствии с формулами (1) и (2), оптимальные стратегии игрока А. По фор-муле (1)

g ₁= 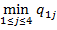= min{7, 6, 5, 4} = 4;

g ₂= 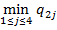= min{1, 8, 2, 3} = 1;

g ₃= 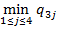= min{8, 1, 3, 2} = 1.

По формуле (2) 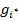= max{4, 1, 1}, откуда следует, что оптимальная стратегия i * = 1 и нижняя цена игры V ^-= 4.

Найдём, в соответствии с формулами (3) и (4), оптимальные стратегии игрока В. По фор-муле (3)

f ₁= 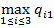= max{7, 1, 8} = 8;

f ₂= 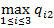= max{6, 8, 1} = 8;

f ₃= 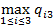= max{5, 2, 3} = 5;

f ₄= 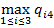= max{4, 3, 2} = 4.

По формуле (4) = min{8, 8, 5, 4} = 4, откуда следует, что оптимальная стратегия j * = 4 и верхняя цена игры V ⁺= 4.

Таким образом, нижняя цена игры совпадает с верхней ценой. Как и должно быть по ут-верждению 1, цена игры 4 равна 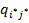= q ₁₄. Пара стратегий á1, 4ñ является решением игры и седловой точкой матрицы Q ■

Пример 2. Рассмотрим матричную игру двух лиц со следующей платёжной матрицей:

Q = , (8)

все элементы которой, кроме q ₂₄, совпадают с соответствующими элементами платёжной матрицы из примера 1.

Найдём, в соответствии с формулами (1) и (2), оптимальные стратегии игрока А. По фор-муле (1)

g ₁= 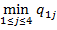= min{7, 6, 5, 4} = 4;

g ₂= 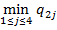= min{1, 8, 2, 5} = 1;

g ₃= 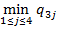= min{8, 1, 3, 2} = 1.

По формуле (2) 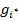= max{4, 1, 1}, откуда следует, что оптимальная стратегия i * = 1 и нижняя цена игры V ^-= 4.

Найдём, в соответствии с формулами (3) и (4), оптимальные стратегии игрока В. По фор-муле (3)

f ₁= 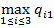= max{7, 1, 8} = 8;

f ₂= 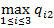= max{6, 8, 1} = 8;

f ₃= 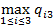= max{5, 2, 3} = 5;

f ₄= 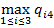= max{4, 5, 2} = 5.

По формуле (4) = min{8, 8, 5, 5} = 5, откуда следует, что множеством оптимальных страте-гий j * является множество {3, 4} и верхняя цена игры V ⁺ = 5.

Таким образом, в данном случае, в отличие от примера 1, нижняя цена игры не равна верхней цене. Поэтому для данной платёжной матрицы Q решений игры, как и седловых точек, нет ■

Для любой матричной игры верно следующее

Утверждение 2. При прибавлении любого числа a (положительного или отрицательного) ко всем элементам платёжной матрицы Q множества оптимальных стратегий обоих игроков не изменяются, а нижняя и верхняя цена игры получены из исходных прибавлением того же числа a ■

В силу утверждения 2 существование решения игры также не зависит от прибавлении ко всем элементам платёжной матрицы Q произвольной константы.

Задание 1. В играх с указанными платёжными матрицами найти оптимальные стратегии обоих игроков, нижнюю и верхнюю цены игры. Указать решение игры, если оно есть; в противном случае явно указать на его отсутствие. В качестве образца см. примеры 1 и 2

				-99

				-23

-19
				-90

	-15
			-13

	-19
		-18
			-29

		-30

		-19

	-13
		-27

■

Дата добавления: 2015-10-16