Обобщённые паросочетания

В главе 6 было введено понятие двудольного графа. Далее, в главе 9, рассматривались свя-занные с такими графами задача о максимальном паросочетании и задача назначения. В этих за-дачах вершины одной доли графа интерпретируются как исполнители, а вершины другой – как задания, которые могут быть выполнены определёнными исполнителями. При поиске паросоче-тания требовалось обеспечить максимальную эффективность соответствующего назначения, т.е. сопоставления работ исполнителям. При этом интересы самих исполнителей не только не принимались во внимание, но даже и не рассматривались.

Однако во многих случаях обеим частям двудольного графа (а не только исполнителям) естественно сопоставляются некоторые интересы. Примером может служить распределение вы-пускников медицинского вуза между больницами, распределение выпускников военной акаде-мии между воинскими частями, и т.д. Другим примером служит распределение рукописей меж-ду рецензентами в научном издательстве. Конечно, рукописи сами по себе не обладают никаки-ми мнениями относительно рецензентов, однако такими мнениями обладают редакторы изда-тельства, которые понимают, какие рецензенты лучше подходят для работы с той или иной ру-кописью.

Общепринято рассматривать ситуации, в которых элементы каждой из двух сторон имеют предпочтения относительно элементов другой стороны, в гендерных терминах. Предполагается, что имеются мужчины и женшины: с точки зрения любого мужчины, все женщины ранжирова-ны от лучшей к худшей, а с точки зрения любой женщины, так же ранжированы все мужчины. Все эти ранжировки могут быть совершенно произвольными.

Задача брачного агенства состоит в поиске разумного паросочетания (об оптимальных в такой деликатной ситуации вряд ли стоит говорить). Для того, чтобы формализовать понятие разумности паросочетания, рассмотрим некоторые примеры. Здесь и далее предполагается, что участники могут свободно обмениваться информацией о своих предпочтениях, а брачное агент-ство, естественно, знает их все.

Пример 1. Пусть имеется трое мужчин и три женщины, т.е. М = { m ₁, m ₂, m ₃}, W = { w ₁, w ₂, w ₃} и предпочтения участников имеют вид:

P (m ₁) = w ₂, w ₁, w ₃; P (w ₁) = m ₁, m ₂, m ₃

P (m ₂) = w ₁, w ₃, w ₂; P (w ₂) = m ₃, m ₁, m ₂;

P (m ₃) = w ₁, w ₂, w ₃; P (w ₃) = m ₃, m ₁, m ₂.

Это означает, что с точки зрения мужчины m ₁ лучшей является женщина w ₂, за ней следует женщина w ₁ и затем – женщина w ₃; с точки зрения женщины w ₁ лучшим является мужчина m ₁, за ним следует мужчина m ₂ и затем – мужчина m ₃, и т.д. Рассмотрим паросочетание

μ =

и мужчину m ₁. Ему паросочетанием μ предписывается жениться на женщине w ₁, при том, что более предпочтительным для него вариантом является женитьба на w ₂. В то же время женщина w ₂ должна, согласно паросочетанию μ, выйти замуж за m ₂, хотя мужчина m ₁ для неё более предпочтителен. Но тогда пара (m ₁, w ₂)может отказаться принимать условия, предлагаемые па-росочетанием μ, поскольку они оба предпочитают друг друга более, чем предлагаемых им парт-нёров. Если брачное агентство предлагает своим клиентам устроить браки в соответствии с дан-ным паросочетанием μ, то пара (m ₁, w ₂) не будем следовать советам этого агенства ■

В случаях, аналогичных рассмотренному в примере 1, говорят, что пара (m, w) блокиру-ет паросочетание μ. Сама такая пара называется блокирующей паросочетание.

Пример 2. При тех же самых предпочтениях, как в примере 1, рассмотрим паросочетание

ν = .

Рассмотрим мужчину m ₁ и женщину w ₂. Поскольку женщине w ₂ предписан лучший, по её мне-нию, мужчина m ₁, то пара (m ₁, w ₂) не является блокирующей данное паросочетание ν. Пара (m ₁, w ₃) не является блокирующей, поскольку мужчине m ₁ предписана женщина w ₁, которая в его предпочтениях стоит перед женщиной w ₃. Пара (m ₃, w ₃) не является блокирующей, поскольку мужчине m ₃ предписана женщина w ₂, которая в его предпочтениях стоит перед женщиной w ₃. Далее, рассмотрим пару (m ₃, w ₁). Она не является блокирующей, поскольку женщине w ₁ пред-писан лучший, по её мнению, мужчина m ₁. Пара (m ₂, w ₁) не является блокирующей по той же причине (женщине w ₁ предписан лучший, по её мнению, мужчина m ₁). Наконец, пара (m ₂, w ₂) не является блокирующей, поскольку женщине w ₂ предписан лучший, по её мнению, мужчина m ₃.

Таким образом, рассмотрены все 6 пар, которые не предписаны друг другу паросочетанием ν (число таких пар всегда равно 6 при 3-ёх мужчинах и 3-ёх женщинах независимо от паросочета-ния). Ни одна из этих пар не является блокирющей ■

Паросочетание, не содержащее блокирующих пар, называется устойчивым. Пример 2 по-казывает, что при рассматриваемых предпочтениях паросочетание ν является устойчивым. Ус-тойчивость не означает, что все получают лучших – с их точки зрения – партнёров. В паросоче-тании ν каждый мужчина получает 2-ую по своему предпочтению женщину, женщины w ₁ и w ₂ получают лучших – с их точки зрения – партнёров, а женщина w ₃ получает мужчину m ₂, зани-мающего последнее место в её предпочтениях. И тем не менее пары, которая блокировала бы это паросочетание, нет.

Естественно возникающие вопросы состоят в следующем. Существует ли хотя бы одно устойчивое паросочетание состояние при любых предпочтениях участников? Как его найти, ес-ли оно существует? На 1-ый вопрос положительный ответ даёт

Утверждение 1. При любых предпочтениях участников, задаваемых строгими ранжиров-ками, устойчивые паросочетания существуют ■

Приведём алгоритм построения устойчивого паросочетания. Доказательство утверждения 1 (которое здесь не приводится) как раз и состоит в доказательстве того, что паросочетание, по-строенное данным алгоритмом, действительно устойчиво. Для упрощения изложения алгоритм демонстрируется на конкретном примере.

Пример 3. Построить устойчивое паросочетание при заданных предпочтениях мужчин и женщин. Пусть имеется трое мужчин и четыре женщины, т.е. М = { m ₁, m ₂, m ₃}, W = { w ₁, w ₂, w ₃, w ₄} и предпочтения участников имеют вид:

P (m ₁) = w ₂, w ₁, w ₄, w ₃; P (w ₁) = m ₂, m ₁, m ₃;

P (m ₂) = w ₂, w ₃, w ₄, w ₁; P (w ₂) = m ₃, m ₂, m ₁;

P (m ₃) = w ₁, w ₄, w ₃, w ₂; P (w ₃) = m ₃, m ₁, m ₂;

P (w ₄) = m ₁, m ₃, m ₂.

Алгоритм состоит из последовательно выполняемых шагов 1, 2, 3, …. Каждый шаг состо-ит из двух фаз: фазы приписывания (А) и фазы отказа (Б). В фазе приписывания каждому мужчине из тех, у кого на данный момент нет пары, приписывается женщина, следующая в его предпочтении сразу после той, которая отказала ему (отвергла его) на предыдущем шаге. (На шаге 1 в фазе приписывания каждому мужчине просто приписывается первая в его предпочте-нии женщина.)

Если на каком-то шаге после фазы приписывания всем мужчинам приписаны разные жен-щины, то искомое паросочетание найдено и алгоритм прекращает работу. В противном случае переходим к фазе отказа.

В фазе отказа каждая женщина из тех, которым приписано более одного мужчины, остав-ляет того мужчину, который предшествует остальным из приписанных ей. Этот мужчина обра-зует с данной женщиной пару, а остальным она отказывает (отвергает их).

Посмотрим, как работает алгоритм в рассматриваемом случае.

Шаг 1.

Фаза А. Приписываем каждому мужчине предпочитаемую им женщину. Получим

.

Фаза Б. Женщине w ₂ приписано двое мужчин: m ₁ и m ₂. Поскольку в её предпочтении m ₂ пред-шествует m ₁, то она отвергает m ₁. Получаем «неполное» паросочетание

.

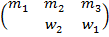Запомним, что мужчину m ₁ отвергла женщина w ₂.

Шаг 2.

Фаза А. В данный момент у мужчины m ₁ нет пары. В соответствии с алгоритмом приписываем ему женщину, следующую в его списке сразу после отвергшей его женщиной w ₂. Таковой явля-ется женщина w ₁. В результате приписывания получаем

.

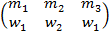Фаза Б. Женщине w ₁ приписано двое мужчин: m ₁ и m ₃. Поскольку в её предпочтении m ₁ пред-шествует m ₃, то она отвергает m ₃. Получаем «неполное» паросочетание

.

Запомним, что мужчину m ₃ отвергла женщина w ₁.

Шаг 3.

Фаза А. В данный момент у мужчины m ₃ нет пары. В соответствии с алгоритмом приписываем ему женщину, следующую в его списке сразу после отвергшей его женщиной w ₁. Таковой явля-ется женщина w ₄. В результате приписывания получаем

.

Поскольку всем мужчинам сопоставлены разные женщины, то искомое паросочетание найдено и алгоритм прекращает работу. В результате мужчина m ₂ получает предпочитаемую им женщину, мужчины m ₁ и m ₃ получают женщин w ₁ и w ₄, вторых по их предпочтениям. Женщи-нам w ₁, w ₂ и w ₄ достаются мужчины m ₁, m ₂ и m ₃, вторые по их предпочтениям. Женщина w ₃ остаётся одна ■

В рассмотренном примере на 1-ом шаге в фазе приписывания женщины приписывались мужчинам. Можно использовать тот же алгоритм, в котором женщины заменены на мужчин, а мужчины на женщин, т.е. на 1-ом шаге мужчины приписываются женщинам, далее на фазе от-каза из нескольких женщин, приписанных одному мужчине, остаётся та, которая предпочти-тельней остальных, и т.д. Возможно построить несколько устойчивых паросочетаний, некото-рые из которых могут быть в каких-то отношениях лучше, чем данное. Однако используемый алгоритм гарантирует устойчивость полученного паросочетания (отсутствие блокирующих пар) при любых исходных данных.

Можно сказать, что брачное агентство является в данном случае метаигроком, который определяет правила взаимодействия участников: они указывают свои предпочтения (в виде строгих ранжировок), а участникам предлагается достаточно разумное устойчивое паросочета-ние, которое строится на основе полученной от участников информации об их предпочтениях. В большинстве случаев такие разумные (в данном случае – устойчивые) паросочетания опреде-ляются неоднозначно, однако вопрос о том, как их оценивать и как выбирать в том или ином смысле «лучшие» или «оптимальные» паросочетания, здесь не рассматривается.

Задание 1. Построить, пользуясь рассмотренным выше алгоритмом, устойчивые паросо-четания при следующих предпочтениях участников:

P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 2, m 1; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 1, m 2.	P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 1, m 3; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 1, m 2.
P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 2, m 1; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 1, m 2.	P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 1, m 3; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 1, m 2.
P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 1, m 2.	P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 1, m 2.
P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 1, m 2; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 2, m 1.	P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 3, m 1; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 2, m 1.
P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 1, m 2; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 2, m 1.	P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 3, m 1; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 2, m 1.
P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 2, m 1.	P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 2, m 1.
P (m 1) = w 2, w 1, w 3; P (w 1) = m 3, m 2, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 2, m 3, m 1; P (m 3) = w 1, w 3, w 2; P (w 3) = m 2, m 3, m 1.	P (m 1) = w 2, w 1, w 3; P (w 1) = m 3, m 2, m 1; P (m 2) = w 1, w 3, w 2; P (w 2) = m 2, m 3, m 1; P (m 3) = w 2, w 3, w 1; P (w 3) = m 2, m 3, m 1.
P (m 1) = w 1, w 3, w 2; P (w 1) = m 3, m 2, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 2, m 3, m 1; P (m 3) = w 2, w 1, w 3; P (w 3) = m 2, m 3, m 1.	P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 2, m 1; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 1, m 2.
P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 1, m 3; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 1, m 2.	P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 2, m 1; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 1, m 2.
P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 1, m 3; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 1, m 2.	P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 1, m 2.
P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 2, m 1; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 1, m 2.	P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 1, m 2; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 2, m 1.
P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 3, m 1; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 2, m 1.	P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 1, m 2; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 2, m 1.
P (m 1) = w 2, w 1, w 3; P (w 1) = m 2, m 3, m 1; P (m 2) = w 1, w 3, w 2; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 2, m 1.	P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 1, w 3; P (w 3) = m 3, m 2, m 1.
P (m 1) = w 1, w 3, w 2; P (w 1) = m 2, m 3, m 1; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 1, m 2; P (m 3) = w 2, w 3, w 1; P (w 3) = m 3, m 2, m 1.	P (m 1) = w 2, w 1, w 3; P (w 1) = m 3, m 2, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 1, m 3, m 2; P (m 3) = w 1, w 3, w 2; P (w 3) = m 2, m 3, m 1.
P (m 1) = w 2, w 1, w 3; P (w 1) = m 3, m 2, m 1; P (m 2) = w 1, w 3, w 2; P (w 2) = m 1, m 3, m 2; P (m 3) = w 2, w 3, w 1; P (w 3) = m 2, m 3, m 1.	P (m 1) = w 1, w 3, w 2; P (w 1) = m 3, m 2, m 1; P (m 2) = w 2, w 3, w 1; P (w 2) = m 1, m 3, m 2; P (m 3) = w 2, w 1, w 3; P (w 3) = m 2, m 3, m 1.
P (m 1) = w 1, w 3, w 2; P (w 1) = m 3, m 2, m 1; P (m 2) = w 2, w 1, w 3; P (w 2) = m 1, m 3, m 2; P (m 3) = w 2, w 3, w 1; P (w 3) = m 2, m 3, m 1.	P (m 1) = w 2, w 3, w 1; P (w 1) = m 2, m 1, m 3; P (m 2) = w 2, w 1, w 3; P (w 2) = m 3, m 2, m 1; P (m 3) = w 1, w 3, w 2; P (w 3) = m 3, m 1, m 2.

■

Дата добавления: 2015-10-16