
|
Читайте также: |
Ідентифікуємо змінні:
Y - витрати на харчування (залежна змінна);
Х (х1, х2) - незалежні змінні: х1 - загальні витрати, г.о.; х2 - розмір сім'ї (кількість членів сім'ї).
Практикою спостережень, наприклад, встановлено, що дана модель може бути специфікована у лінійній формі:
де Y, 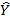 - відповідно фактичні та розрахункові значення тижневих витрат на харчування за моделлю; u - залишки;
- відповідно фактичні та розрахункові значення тижневих витрат на харчування за моделлю; u - залишки; 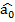 ,
, 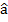 1,
1, 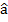 2 - оцінка параметрів моделі.
2 - оцінка параметрів моделі.
Оператор оцінки параметрів моделі а}- при використанні 1МНК має вигляд:

Х΄- матриця, транспонована до Х.
Одиниця в матриці незалежних змінних X дописується тоді, коли економетрична модель має вільний член а0 (як у нашому випадку).
Згідно з оператором оцінювання обчисляємо матриці:
Отже, економетрична модель множинної регресії для тижневих витрат на харчування запишеться так:
Зробимо економетричні висновки.
Коли за всіх однакових умов незалежна змінна х1 (загальні витрати) змінюється (збільшується або зменшується) на одиницю, то залежна змінна У змінюється на 0,2 одиниць. Якщо при тих же умовах незалежна змінна х2 (розмір сім'ї) змінюється на одиницю, то залежна змінна У змінюється на 6,97 одиниць.
Визначимо множинні коефіцієнти детермінації та кореляції:
| № з/п | У | 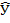
| (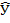 - -  ) 2 ) 2
| (У -  ) 2 ) 2
| u =
= У - 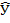
| u2 =
= (У - 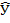 ) 2 ) 2
|
| 2 | 6 | |||||
| 20,3 | 1,7 | 2,89 | ||||
| 27,0 | ||||||
| 39,0 | ||||||
| 58,0 | ||||||
| 42,9 | 4,1 | 16,81 | ||||
| 55,1 | 10,9 | 118,8 | ||||
| 69,9 | 18,5 | 11,1 | 123,2 | |||
| 96,8 | 132.2 | 9,2 | 84,6 | |||
| 66,1 | 3,9 | 15,21 | ||||
| 82,0 | 10,9 | 94,1 | ||||
| 104,6 | 14,4 | 207,4 | ||||
| 131,7 | 11,3 | 127,7 | ||||
| 95,0 | 94,1 | 59,3 | -2 | |||
| 119,6 | 13,4 | 179,6 | ||||
| 150,8 | 18,2 | 331,2 | ||||
| 202,0 | -5 | |||||
| І | 1364,8 | - | 1656,4 | |||
| У середньому | 85,3 | - | - | - | - |
Визначимо коефіцієнти детермінації та кореляції, якщо (n-1)=(16-1)=15 і (n-m1)=(16-3)=13:
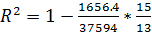 =0.950; R=0.975.
=0.950; R=0.975.
Коефіцієнти детермінації та кореляції наближені до одиниці, тому зв'язок між змінними X та У - тісний. Значення коефіцієнта витрат на харчування на 95% визначається варіаціями загальних витрат та розміром сім'ї, а 5% припадає на невраховані фактори.
Визначимо значимість зв'язку між змінними X та У за допомогою F-критерію Фішера
 =
= 
Обчислене фактичне значення критерія Фішера F порівнюється з табличним Fтабл, (див. додаток А). При ступенях вільності чисельника (m1-1)=(3-1)=2 та знаменника (n-m1)=(16-3)=13 і прийнятому рівню довіри (1-α)=(1-0,05)=0,95 Fтабл для розглянутої моделі дорівнює Fтабл =3,81. Так як F>Fтавл (141,0>3,81), то це означає значимість зв'язку в економетричній моделі.
Для перевірки значимісті коефіцієнта кореляції R розраховуємо t-критерій Ст'юдента:
З використанням статистичних таблиць (додаток Б) при рівні значимості α =0,05 та числу ступенів вільності (n-m1)=(16-3)=13 вибираємо tтабл =1,771.
Оскільки t α > tтабл, то можна зробити висновок про значимість коефіцієнта кореляції.
Для оцінки значимості оцінок параметрів моделі множинної регресії обчислимо t-критерій. Дисперсія залишок дорівнює
 =
= 
Тоді з урахуванням стандартної помилки оцінки параметрів розраховуєм значення t-критеріїв:
Вище було визначене табличне значення t-критерію tтабл=1,771. Порівняння розрахованих та табличного значень t-критеріїв приводить до такого: t1α <tтабл, що свідчить про нестійкість впливу змінної х1 на результативну ознаку У; t2α <tтабл. та t3α <tтабл, що показує істотний зв'язок цих залежних змінних (х2, х3) на залежну У.
На основі t-критеріїв та стандартної помилки
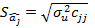 можуть бути визначені довірчі інтервали для параметрів моделі:
можуть бути визначені довірчі інтервали для параметрів моделі:
Так як значення стандартних помилок Saj не перевищують абсолютні значення оцінок параметрів  j, то це означає, що оцінки параметрів є незміщеними.
j, то це означає, що оцінки параметрів є незміщеними.
Нарешті, побудуємо точковий та інтервальний прогнози для економетричної моделі.
Визначимо прогнозне значення залежної змінної при
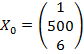 .
.
Тоді М(Y0) можна розглядати як оцінку прогнозного значення математичного сподівання та індивідуального значення витрат на харчування при відомих загальних витратах х1 та розміру сім'ї х2.
Получимо інтервальний прогноз математичного сподівання М(Y0).
Визначимо для цього дисперсію прогнозну  з урахуванням матриці охибок (X`X)-1, яка для розглядаємого прикладу має наведений вигляд:
з урахуванням матриці охибок (X`X)-1, яка для розглядаємого прикладу має наведений вигляд:
Елементи дисперсійно-коваріаційної матриці за формулами мають значення:

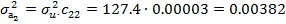
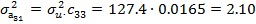

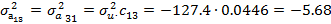

Тоді дисперсіно-коваріаційна матриця запишеться у
вигляді:
Знайлемо дисперсію помилок: 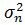 =
= 
Стандартна помилка прогнозу математичного сподівання М(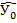 ):
):
Тоді інтервальний прогноз математичного сподівання М(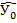 )буде вмежах:
)буде вмежах:
Обчислимо дисперсію та стандартну помилку прогнозу індивідуального значення У0:
Визначимо індивідуальний прогноз індивідуального значення У0:
Отже, при  =0,05 рівні довіри (1-
=0,05 рівні довіри (1-  )=0,95, що відповідає ймовірності р=0,95, прогноз математичного сподівання М(У0) потрапляє в інтервал [103,8; 197,4], а прогноз індивідуального значення - в інтервал [99,8; 201,4]. В економічної інтерпретації це означає, що при прогнозних загальних витратах у 500 одиниць при сім'ї з шести осіб середні витрати на харчування потрапляють в інтервал 103,8
)=0,95, що відповідає ймовірності р=0,95, прогноз математичного сподівання М(У0) потрапляє в інтервал [103,8; 197,4], а прогноз індивідуального значення - в інтервал [99,8; 201,4]. В економічної інтерпретації це означає, що при прогнозних загальних витратах у 500 одиниць при сім'ї з шести осіб середні витрати на харчування потрапляють в інтервал 103,8 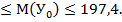
Водночас окремі інтервальні витрати містяться в інтервали 99,8 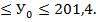
Дата добавления: 2015-10-16; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Оцінка тісноти та значимості зв'язку між змінними у множинній регресії | | | Ознаки мультиколінеарності |