Оцінка тісноти та значимості зв'язку між змінними у множинній регресії

Тіснота зв'язку загального впливу всіх незалежних змінних X на залежну змінну Y визначається коефіцієнтами детермінації і множинної кореляції, а також парними коефіцієнтами кореляції.

Коефіцієнт детермінації характеризує, якою мірою варіація залежної змінної Y визначається варіацією незалежних змінних X.

Вигляд коефіцієнта детермінації у множинній регресії ідентичний коефіцієнту детермінації простої регресії. Оскільки введення нових незалежних змінних х_і (і=1...m) у множинну регресію, а значить і ступенів вільності моделі, приводить до зменшення коефіцієнта детермінації, то його розрахунок повинен бути відкорегований з урахуванням ступенів вільності дисперсії залишок та загальної дисперсії:

,

де 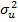- дисперсія залишок ; 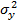– загальна дисперсія моделі .

Підстановка залежностей для дисперсій у формулу для коефіцієнта детермінації R² дає його вираз в залежності від ступенів вільності:

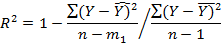
де (n-m₁) та (n-1) - ступені вільності чисельника та знаменника залежності.

Числові значення коефіцієнта детермінації лежать у діапазоні від 0 до 1. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Якщо виникає потреба в оцінкі точності моделі за рахунок кількості незалежних змінних, то це можна здійснити за допомогою нормованого (оціненого) коефіцієнта детермінації,

який має вид

aбо

Множинний коефіцієнт кореляції R розраховується за формулою: R = . Для нього характерна така сама зміна числового значення, як і для коефіцієнта детермінації.

Парні коефіцієнти кореляції дають оцінку тісноти зв'язку між парами змінних: залежною у та незалежною x_j змінними r_yxj; незалежними змінними х_к та x_j – r

Розраховуються вони за формулами:

= ,

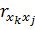Де n- кількість спостережень; y^*,x_j^*,x_k^* - нормалізовані (стандартизовані) змінні.

; = ; ;

–середні значення залежної та незалежної змінних;

– середньоквадратичні відхилення змінних.

Інформацію про парну залежність може дати симетрична матриця коефіцієнтів парної регресії між пояснювальними змінними:

Значимість зв'язку між залежною Y та залежними змінними X у випадку множинної регресії можна перевірити за допомогою F-критерія Фішера:

Де (m₁-1) – ступені вільності загальної дисперсії (стиупені вільності чисельника); (n-m1) - ступені вільності дисперсії залишок (ступені вільності знаменника).

Фактичне значення F-критерія Фішера порівнюється з табличним при ступенях вільності (т₁-1) і (п-т₁) та вибраному рівню значимості α. Якщо F>F_табл., то гіпотеза про значимість зв'язку між залежною та незалежними змінними множинної регресії підтверджується, у противному разі - відкидається.

Значимість коефіцієнта кореляції та оцінок параметрів моделі множинної регресії

У кореляційному аналізі для характеристики відхилень коефіцієнта кореляції, як вибіркової величини, від свого "істотного" значення вимагається перевірка його значимості за t - критерієм Ст'юдента:

де R² - коефіцієнт детермінації моделі; R - коефіцієнт кореляції; (п-т₁) - число ступенів вільності.

Розраховане за цією формулою фактичне значення (­критерію зіставляється з табличним значенням t_табл. Останнє обирається за статистичними таблицями на підставі прийнятого рівня значимості α та розрахованого числа ступеней вільності (п-т₁). Якщо t _α > t_табл, то можна зробити висновок про значимість коефіцієнта кореляції між змінними.

У кореляційному аналізі може перевірятись також

значимість оцінок параметрів моделі із знаходженням їх довірчих інтервалів.

Припустивши, що залишки и розподілені за нормальним законом, приймається, що параметри моделі також задовольняють нормальному розподілу. Тоді перевірку гіпотези про значимість оцінок параметрів моделі проводять згідно з t - критерієм Ст'юдента:

де 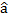_j - індивідуальні параметри матриці (j= 1,2,…,m_j); 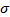² _u - дисперсія залишків; с_jj - діагональний елемент матриці (X`X)^-1; – стандартна помилка оцінки параметра моделі.

Обчислене значення t -критерію порівнюється з табличним t_табл, при вибраному рівні значимості α і (n-m₁) ступенях вільності. Якщо t _α > t_табл, то оцінка значимості відповідного параметру моделі є достовірною.

На підставі t-критерію і стандартної помилки встановлюються довірчі інтервали для параметра а_j:

Коли стандартні помилки параметрів 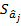не перевищують абсолютні значення цих параметрів , то це може означати, що оцінки параметрів є незміщеними відносно їх істотних значень.

Приклад. Побудувати економетричну модель множинної регресії, яка описує зв'язок між тижневими витратами на харчування, загальними витратами та розміром сім'ї. Оцінити тісноту та значимість зв'язку між змінними та параметрами моделі. Дані обстеження сімей наведені у таблиці:

№	Витрати на харчування	Загальні витрати	Розмір сім’ї (кількість)
			1,5
			1,6
			1,9
			1,8
			3,4
			3,6
			3,4
			3,5
			5,5
			5,4
			5,4
			5,3
			8,5
			8,3
			8,1
			7,3

Розрахувати точковий та індивідуальний прогнози математичного сподівання індивідуального значення залежної змінної, коли для прогнозного періоду відомий вектор

.

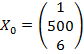Дата добавления: 2015-10-16